MySQL索引底层实现

一、引入

索引的概念：索引是可以快速获取数据的数据结构。

那么既然是数据结构，用什么数据结构实现呢？

首先对于下面的表 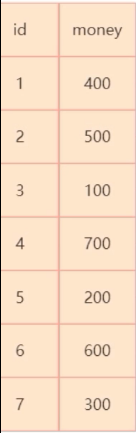如果执行语句 select * from t where t.money = 300;，需会全表扫描，一条一条的遍历查询。

查询一行数据至少和磁盘做一次I/O操作（I/O是很耗性能的），至少要做 7 次 I/O 操作。

二、索引的数据结构

1）AVL树

那么利用AVL树的特性，将数据划分为两部分，可以降低时间复杂度。

图示是最好的情况，近似于折半查找，时间复杂度为O(log2n)。但对于特殊数据，组成不平衡的AVL树，退化为顺序查找，效率为O(n)。

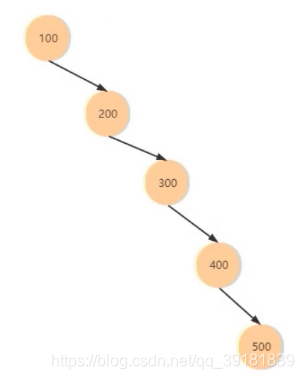
2）红黑树

当单边的节点大于3时候，红黑树就会自动调整，这样可以解决二叉树的弊端。

但是红黑树同样也有弊端：

• 当数据量特别大的时候，红黑树的高度特别大。

• 有可能查询的数据在叶子节点，那查询的次数也很大，且进行多次磁盘I/O操作，性能差。

3） B树

多路平衡查找树，M阶B树代表每个节点最多可以有M个子节点，所有非叶子节点在同一层。

B树有以下特点：

• 每个节点中的关键字都按照从小到大的顺序排列，每个关键字的左子树中的所有关键字都小于它，而右子树中的所有关键字都大于它。
• 所有叶子节点都位于同一层，并且叶子节点只有关键字，指向孩子的指针都为null。
• 每个节点都存有索引和数据，也就是对应的key和value。

B树查找数据的时间复杂度最好为O(1)，即在第一个节点就查到，最差为O(logN)。

B树的弊端： 若一个节点的空间为16KB，若data中的数据过大，则一个节点能放的数据量较小，这样就会造成树的高度比较大（比红黑树高度小点）

4） B+树

B+ Tree 是基于 B Tree 和叶子节点顺序访问指针进行实现，它具有 B Tree 的平衡性，并且通过顺序访问指针来提高区间查询的性能。

B+树与B树的区别：

• B+树的非叶子节点只存储索引，不存储data，可以放更多索引
• 叶子节点包含所有索引字段，所有的data元素都存储在叶子节点

• 叶子节点使用指针连接，对 select * from t where col2 > 20 的范围查找更快速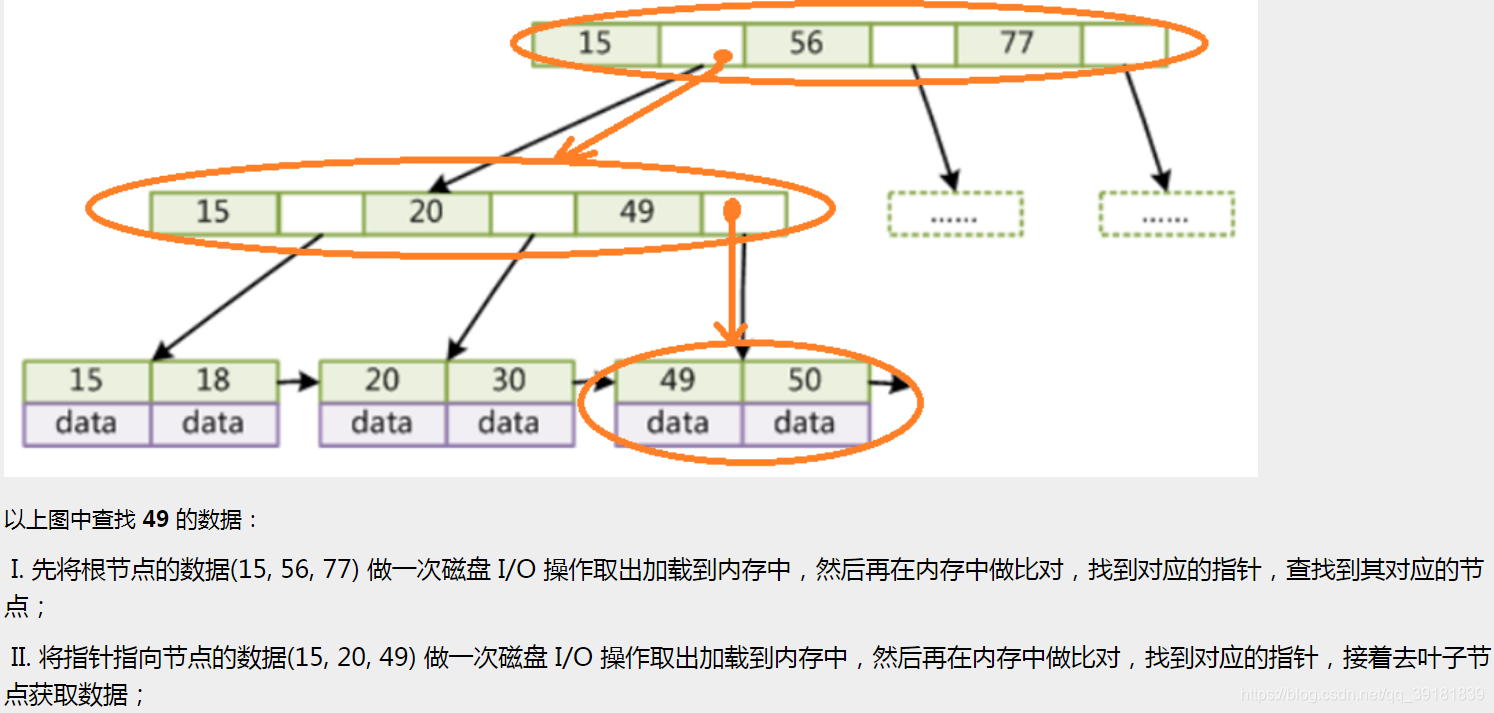

• 时间复杂度固定为O(logN)