LeetCode刷题—回文问题

由一个整数问题引入。

回文即 正序（从左向右）和倒序（从右向左）读都是一样的。常见的有整数、链表、字符串相关问题。

先由整数问题引入。

回文数

7，整数反转，easy

给你一个 32 位的有符号整数 x ，返回 x 中每位上的数字反转后的结果。

如果反转后整数超过 32 位的有符号整数的范围 [−2³¹, 2³¹ − 1] ，就返回 0。

假设环境不允许存储 64 位整数（有符号或无符号）。

示例 1：

输入：x = 123
输出：321

示例 2：

输入：x = -123
输出：-321

题解

此题需要注意的是x的范围，x∈[-2147483648, 2147483647]

考虑整数反转，只要不断取余并 / 10，即可取出末尾数字并构成新的反转数。如：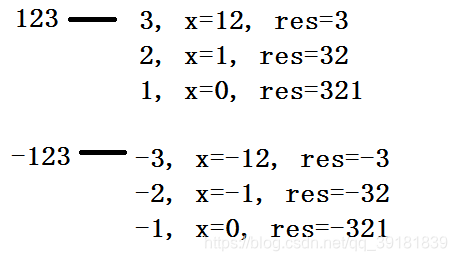

可见此方法适用于 x为正或为负，循环的判断条件为 x != 0 即可。

但是需要注意的是 反转数 的范围，比如 x = 1147483619，反转后超过[−2³¹, 2³¹ − 1]。则需要判断临界条件，判断第一次取余后的x

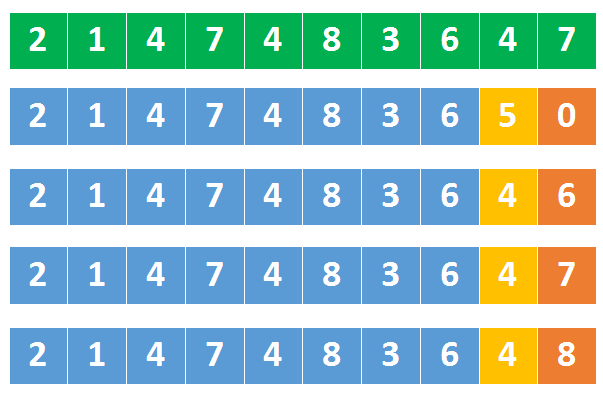
如图，如果此时x > 214748364 说明已经超过范围，返回 0；如果此时x = 214748364，需要比较刚取出的末位数字与 7 的关系

负数同理

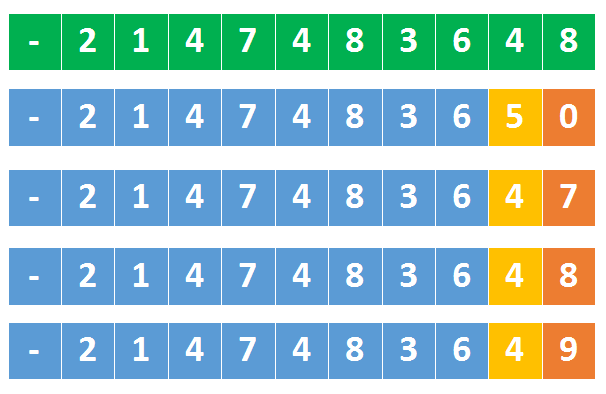
代码

class Solution {
    public int reverse(int x) {
        // x ≥ -2147483648 && x ≤ 2147483647
        //将整数x不断取模，再x/10
        //x可正可负，判断条件为！= 0
        int res = 0;
        while(x != 0){
            int tmp = x % 10;//取模结果可正可负
            //判断剩余值是否越界
            if(res > 214748364 || res == 214847364 && tmp > 7){
                return 0;
            }
            if(res < -214748364 || res == -214748364 && tmp < -8){
                return 0;
            }
            //新的结果
            res = res * 10 + tmp;
            x /= 10;
        }
        return res;
    }  
}

有了这道题的思路，那么判断一个整数是否为回文数就很简单了，只需进行反转然后比较与原数字是否相等。

9，回文数，easy

判断一个整数是否是回文数。回文数是指正序（从左向右）和倒序（从右向左）读都是一样的整数。

示例 1:

输入: 121
输出: true

示例 2:

输入: -121
输出: false
解释: 从左向右读, 为 -121 。 从右向左读, 为 121- 。因此它不是一个回文数。

代码

class Solution {
    public boolean isPalindrome(int x) {
        if(x < 0) return false;
        int res = 0;
        int cur = x;
        while(x != 0){
            int tmp = x % 10;
            if(res > 214748364 || res == 214748364 && tmp > 7){
                return false;
            }
            if(res < -214748364 || res == -214748364 && tmp < -8){
                return false;
            }
            res = res * 10 + tmp;
            x /= 10; 
        }
        return res == cur;
    }
}

回文串

有了上面判断整数是否回文，再看字符串的问题。

125，验证回文串，easy

给定一个字符串，验证它是否是回文串，只考虑字母和数字字符，可以忽略字母的大小写。

说明：本题中，我们将空字符串定义为有效的回文串。

示例 1:

输入: "A man, a plan, a canal: Panama"
输出: true

示例 2:

输入: "race a car"
输出: false

题解

回文常用左右指针来判断

此题难点在于只考虑字母和数字且忽略字母大小写，要进行合法字符的判断再用快慢指针比较字符是否相同。

代码

class Solution {
    public boolean isPalindrome(String s) {     
        //首先将s转为没有空格全部小写的字符串
        StringBuilder sb = new StringBuilder();
        for(int i = 0; i < s.length(); i++){
            char c = s.charAt(i);
            if(c == ' ') continue;
            else if(c >= 'A' && c <= 'Z'){
                sb.append(Character.toLowerCase(c));
            }else if(c >= 'a' && c <= 'z' || c >= '0' && c <= '9'){
                sb.append(c);
            }
        }

        int left = 0;
        int right = sb.length() - 1;
        while(left < right){
            if(sb.charAt(left)==(sb.charAt(right))){
                left++;
                right--;
            }else{
                return false;
            }
        }
        return true;
    }
}

对于回文串，也常用动态规划来求最XX个数。

如下两道题。

647，回文子串，medium

给定一个字符串，你的任务是计算这个字符串中有多少个回文子串。

具有不同开始位置或结束位置的子串，即使是由相同的字符组成，也会被视作不同的子串。

示例 1：

输入："abc"
输出：3
解释：三个回文子串: "a", "b", "c"

示例 2：

输入："aaa"
输出：6
解释：6个回文子串: "a", "a", "a", "aa", "aa", "aaa"

题解

题目中要求回文子串个数，维护一个变量cnt，找到回文子串就将cnt+1

1. 子问题

   \(dp[i][j]\) —— s[i]到s[j]形成的字符串是否是回文串

2. base case

   单个字符一定为回文，返回TRUE

   \(dp[i][i] = true;\)

3. 递推关系

   如果 s[i]==s[j]，则比较中间部分是否是一个回文字符串

   • j - i <= 2，中间不含或只含一个子串，dp[i][j] = true
   • 否则，\(dp[i][j]\) 取决于 \(dp[i+1][j - 1]\)。注意遍历顺序！可以像如图 ：i 从下至上，j 从左至右遍历。

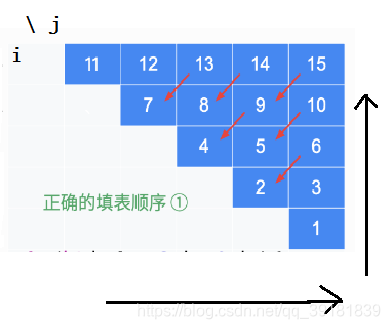
   4. 返回值

      上面得到的 \(dp[i][j]\) 如果为 true，cnt++。最后返回cnt的值。

代码

class Solution {
    public int countSubstrings(String s) {
        int len = s.length();
        if(len == 0) return 0;
        int cnt = 0;
        boolean[][] dp = new boolean[len][len];
        for(int i = 0; i < len; i++){
            dp[i][i] = true;
        } 
        //求dp[i][j]需要通过dp[i+1][j-1] 遍历顺序从下到上，从左到右
        for(int i = len - 1; i >= 0; i--){
            for(int j = i; j < len; j++){
                if(s.charAt(i) == s.charAt(j) && (j - i <= 2 || dp[i + 1][j - 1])){
                    cnt++;
                    dp[i][j] = true;
                }
            }
        }
        return cnt;
    }
}

5，最长回文子串，medium

给你一个字符串 s，找到 s 中最长的回文子串。

示例 1：

输入：s = "babad"
输出："bab"
解释："aba" 同样是符合题意的答案。

示例 2：

输入：s = "cbbd"
输出："bb"

示例 3：

输入：s = "a"
输出："a"

示例 4：

输入：s = "ac"
输出："a"

题解

看到最长联想到用动态规划解题。

1. 子问题

   \(dp[i][j]\) ——子串s[i...j] （闭区间）是否为回文子串

2. 递推关系

   1. base case

      单个字符一定为回文，返回TRUE

      \(dp[i][i] = true;\)

   2. 状态转移方程

      由题意，s[i] == s[j] 时子串s[i...j]为回文；去掉头尾后仍是回文时才有 \(dp[i][j] = true\)。

      则 \(dp[i][j] = (s[i] == s[j]) 与 dp[i+1][j-1]\)。

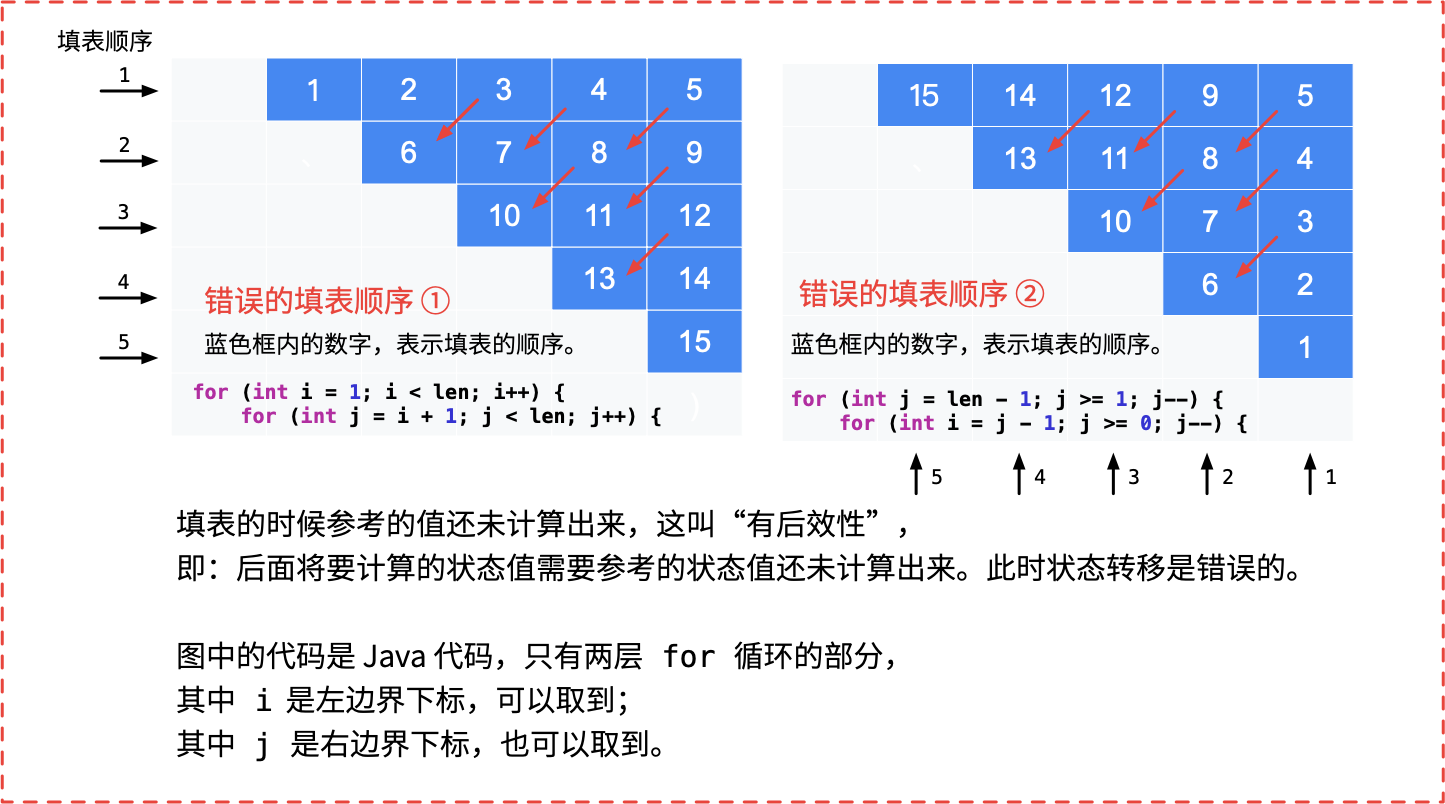
      边界条件： i + 1 ≥ j - 1 => j - i ≤ 2，只需判断 s[i] == s[j]，不用参考以前的 dp值。

      当 j - i > 2 时，需要考虑 \(dp[i+1][j-1]\)，即“有后效性”。在二维表中表现为参考左下方结果才能得到当前的 \(dp\) 值。

3. 返回值

   初始化变量 maxLen 记录最长回文子串长度， start 记录开始位置。

代码

class Solution {
    public String longestPalindrome(String s) {
        if(s.length() < 2) return s;
        int len = s.length();

        boolean[][] dp = new boolean[len][len];
        for(int i = 0; i < len; i++){
            dp[i][i] = true;
        }

        int start = 0;
        int maxLen = 1;

        for(int j = 1; j < len; j++){
            for(int i = 0; i < j; i++){
                if(s.charAt(i) != s.charAt(j)){
                    dp[i][j] = false;
                } 
                else{
                    if(i - j >= -2)
                        dp[i][j] = true; 
                        // dp[i][j] = s.charAt(i) == s.charAt(j);
                    else
                        dp[i][j] = dp[i + 1][j - 1];
                        // dp[i][j] = s.charAt(i) == s.charAt(j) && dp[i + 1][j - 1];
                }
           
                //此时dp[i][j]=true，是回文子串，还要更新开始位置和长度
                if(dp[i][j] && j - i + 1 > maxLen){
                    start = i;
                    maxLen = j - i + 1;
                }
            }
        }
        return s.substring(start, start + maxLen);
    }
}

细节

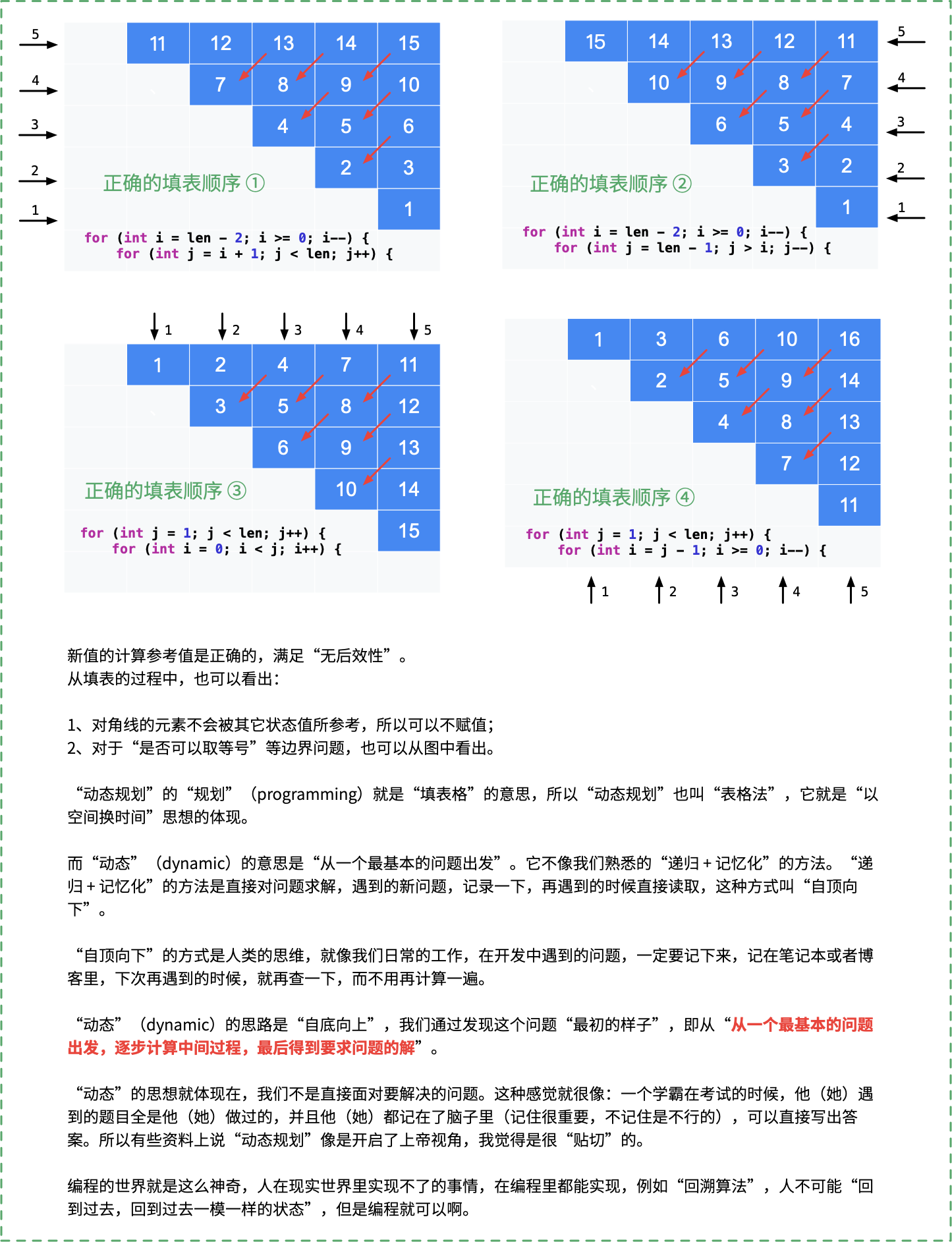
对于填表，由于构成子串，因此 i 和 j 的关系是 i <= j ，因此只需要填这张表格对角线以上的部分。

由于需要满足“无后效性”，填表顺序也需要注意。

说明：表格中的数字表示「填表顺序」，从 1 开始。表格外的箭头和数字也表示「填表顺序」，与表格中的数字含义一致。

回文链表

回文也可以应用在链表中，思路较简单。 #### 234，回文链表，easy

请判断一个链表是否为回文链表。

示例 1:

输入: 1->2
输出: false

示例 2:

输入: 1->2->2->1
输出: true

进阶： 你能否用 O(n) 时间复杂度和 O(1) 空间复杂度解决此题？

题解

利用快慢指针（快速度为慢速度的2倍）找到中间节点，将后半段链表进行反转，再比较反转后的链表与原链表前半段是否相同。

代码

class Solution {
    public boolean isPalindrome(ListNode head) {
        if(head == null) return true;
        ListNode middle = getMiddle(head);//链表中点
        ListNode newHead = reverse(middle.next);//反转后半部分链表
        //比较前半部分和后半部分链表的节点值
        while(newHead != null){
            if(head.val != newHead.val){
                return false;
            }
            head = head.next;
            newHead = newHead.next;
        }
        return true;
    } 
     //返回链表的中间节点（如果链表长度为偶数，为左边的中间节点）
    public ListNode getMiddle(ListNode head){
        ListNode slow = head;
        ListNode fast = head;
        while(fast.next != null && fast.next.next != null){
            slow = slow.next;
            fast = fast.next.next;
        }
        return slow;
    }
    public ListNode reverse(ListNode head){
        if(head == null || head.next == null) return head;
        ListNode temp = reverse(head.next);
        head.next.next = head;
        head.next = null;
        return temp;
    }
}

扩展

此方法符合时间复杂度为 O(n)，空间复杂度为 O(1)。

链表不支持随机访问，从头开始查找，时间复杂度为O(n)，没有用栈等存储，空间复杂度为 O(1)。

链表与数组进行对比：

数组的优点

• 随机访问性强
• 查找速度快

数组的缺点

• 插入和删除效率低
• 可能浪费内存
• 内存空间要求高，必须有足够的连续内存空间。
• 数组大小固定，不能动态拓展

链表的优点

• 插入删除速度快
• 内存利用率高，不会浪费内存
• 大小没有固定，拓展很灵活。

链表的缺点

• 不能随机查找，必须从第一个开始遍历，查找效率低

时间复杂度	数组	链表
读取	O(1)	O(n)
插入	O(n)	O(1)
删除	O(n)	O(1)