LeetCode刷题—贪心算法

发表于 2021-01-31 分类于 LeetCode刷题

概述

贪心算法可以认为是动态规划算法的一个特例，相比动态规划，使用贪心算法需要满足更多的条件（贪心选择性质），但是效率比动态规划要高。

什么是贪心选择性质呢，简单说就是：每一步都做出一个局部最优的选择，最终的结果就是全局最优。注意哦，这是一种特殊性质，其实只有一部分问题拥有这个性质。

比如你面前放着 100 张人民币，你只能拿十张，怎么才能拿最多的面额？显然每次选择剩下钞票中面值最大的一张，最后你的选择一定是最优的。

区间调度问题

先解决一个基础问题：给你很多形如 [start, end] 的闭区间，请你设计一个算法，算出这些区间中最多有几个互不相交的区间。

举个例子，intvs = [[1,3], [2,4], [3,6]]，这些区间最多有 2 个区间互不相交，即 [[1,3], [3,6]]，你的算法应该返回 2。注意边界相同并不算相交。

思路

从区间集合 intvs 中选择一个区间 x，这个 x 是在当前所有区间中结束最早的（end 最小）。

把所有与 x 区间相交的区间从区间集合 intvs 中删除。

重复步骤 1 和 2，直到 intvs 为空为止。之前选出的那些 x 就是最大不相交子集。

步骤

先把每个区间按最后一个元素进行升序排序，其中最小的元素值为x_end，如果后面区间的开始元素比x_end小（即相交），则删除，并更新 x_end。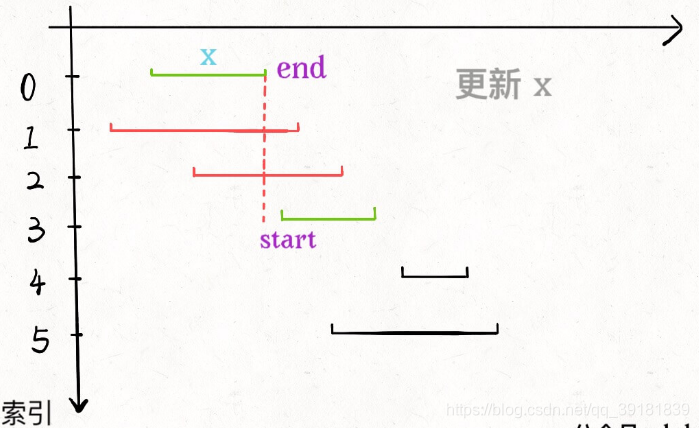在这里插入图片描述

代码

public int intervalSchedule(int[][] intvs) {
    if (intvs.length == 0) return 0;
    // 按 end 升序排序
    Arrays.sort(intvs, new Comparator<int[]>() {
        public int compare(int[] a, int[] b) {
            return a[1] - b[1];
        }
    });
    // 至少有一个区间不相交
    int count = 1;
    // 排序后，第一个区间就是 x，其第二个元素值是 x_end
    int x_end = intvs[0][1];
    for (int[] interval : intvs) {
        int start = interval[0];
        if (start >= x_end) {
            // 找到下一个选择的区间了
            count++;
            x_end = interval[1];
        }
    }
    return count;
}

435，无重叠区间

移除的最小数量，则在上面模板中进行修改。

public int eraseOverlapIntervals(int[][] intervals) {
    if(intervals.length == 0) return 0;
    int n = intervals.length;
    return n - intervalSchedule(intervals);
}

452，用最少数量的箭引爆气球

区间抽象成气球范围，弓箭最小数量即无重叠区间的最大个数（最多有 n 个不重叠的区间，那么就至少需要 n 个箭头穿透所有区间）。与上面模板不同的是，边界相同也算相交。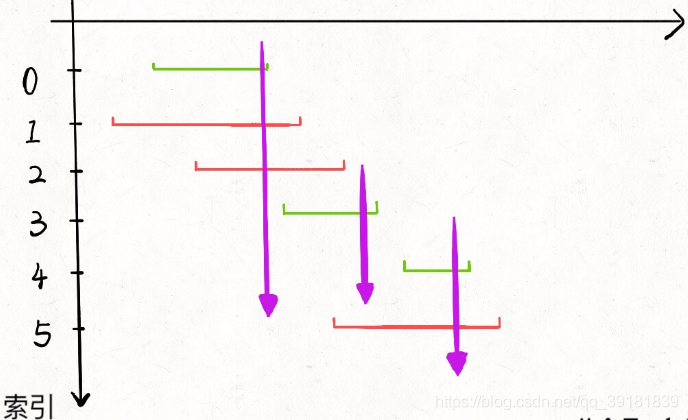在这里插入图片描述

代码

class Solution {
	public int findMinArrowShots(int[][] points) {
        if (points.length == 0) return 0;
        // 按 end 升序排序
        Arrays.sort(points, new Comparator<int[]>() {
            public int compare(int[] a, int[] b) {
                return Integer.compare(a[1], b[1]);
            }
        });
        // 至少有一个区间不相交
        int count = 1;
        // 排序后，第一个区间就是 x，其第二个元素值是 x_end
        int x_end = points[0][1];
        for (int[] point : points) {
            int start = point[0];
            if (start > x_end) {
                // 找到下一个选择的区间了
                count++;
                x_end = point[1];
            }
        }
        return count;
    }
}

其它

455，分发饼干，easy

假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。

对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。

示例 1:

输入: g = [1,2,3], s = [1,1]
输出: 1
解释: 
你有三个孩子和两块小饼干，3个孩子的胃口值分别是：1,2,3。
虽然你有两块小饼干，由于他们的尺寸都是1，你只能让胃口值是1的孩子满足。
所以你应该输出1。

示例 2:

输入: g = [1,2], s = [1,2,3]
输出: 2
解释: 
你有两个孩子和三块小饼干，2个孩子的胃口值分别是1,2。
你拥有的饼干数量和尺寸都足以让所有孩子满足。
所以你应该输出2.

提示：

1 <= g.length <= 3 * 104 0 <= s.length <= 3 * 104 1 <= g[i], s[j] <= 231 - 1

题解

尽可能满足更多的孩子，就不要造成饼干尺寸的浪费。

大尺寸的饼干既可以满足胃口大的孩子也可以满足胃口小的孩子，那么就应该优先满足胃口大的。

这里的局部最优就是大饼干喂给胃口大的，充分利用饼干尺寸喂饱一个，全局最优就是喂饱尽可能多的小孩。

先将饼干和胃口都进行排序，从后向前遍历胃口，用大饼干优先满足胃口大的，并统计满足小孩数量。

代码

class Solution {
    public int findContentChildren(int[] g, int[] s) {
        Arrays.sort(g);
        Arrays.sort(s);
        //最大的饼干
        int i = s.length - 1;
        int count = 0;
        //倒序遍历g，找到能满足胃口的
        for(int j = g.length - 1; j >= 0 && i >= 0; j--){ 
            if(s[i] >= g[j]){
                count++;
                i--;
            }
        }
        return count;
    }
}

也可以从前往后遍历g和s，最小的饼干如果不能满足胃口的话，继续找下一块饼干，如果可以满足，继续比较下一个g 和 s 的元素

class Solution {
    public int findContentChildren(int[] g, int[] s) {
        int i = 0;
        int j = 0;
        int count = 0;
        while(i < s.length && j < g.length){
            if(s[i] >= g[j]){
                count++;
                j++;
            }
            //继续找下一个饼干
            i++;
        }
        return count;
    }
}

121，买卖股票的最佳时机

只允许完成一笔交易（即买入和卖出一支股票一次），计算你所能获取的最大利润。

题解

从左向右遍历时，维护一个最小价格 low，和一个最大利润 maxP，每次比较以当前价格售出时是否为最大利润。

代码

class Solution {
    public int maxProfit(int[] prices) {
		int low = Integer.MAX_VALUE;
        int maxP = 0;
        for(int i = 0; i < prices.length; i++){
            //如果当前价格比low小，更新low
            if(prices[i] < low) low = prices[i];
            //得到每次以当前价格卖出得到的最大利润值
            maxP = Math.max(maxP, prices[i] - low);
        }
        return maxP;
    }
}

122，买卖股票的最佳时机Ⅱ

允许多次交易，进行买入卖出操作。

题解

多次买卖，只要今天的价格比昨天高，就可以在昨天买入今天卖出，保证今天的利润是正的，这样得到的利润值最大。

代码

class Solution {
    public int maxProfit(int[] prices) {        
		if(prices.length < 2) return 0;
        int maxP = 0;
        for(int i = 1; i < prices.length; i++){
            if(prices[i] > prices[i - 1])
                maxP += prices[i] - prices[i - 1];
        }
        return maxP;
    }
}

605，种花问题，easy

假设有一个很长的花坛，一部分地块种植了花，另一部分却没有。可是，花不能种植在相邻的地块上，它们会争夺水源，两者都会死去。

给你一个整数数组 flowerbed 表示花坛，由若干 0 和 1 组成，其中 0 表示没种植花，1 表示种植了花。另有一个数 n ，能否在不打破种植规则的情况下种入 n 朵花？能则返回 true ，不能则返回 false。

示例 1：

输入：flowerbed = [1,0,0,0,1], n = 1
输出：true

示例 2：

输入：flowerbed = [1,0,0,0,1], n = 2
输出：false

提示：

1 <= flowerbed.length <= 2 * 104 flowerbed[i] 为 0 或 1 flowerbed 中不存在相邻的两朵花 0 <= n <= flowerbed.length

题解

能种花的条件有三个：①. 此位置没有种花 ②. 左边没有种花或者当前为最左 ③. 右边没有种花或者当前为最右.

找到这样的位置就种花，计数器count++，最后返回与 n 的比较值。

代码

class Solution {
    public boolean canPlaceFlowers(int[] flowerbed, int n) {      		  int count = 0;
        for(int i = 0; i < flowerbed.length; i++){
            //可以种花的条件：当前位置为空、左边为空或为最左、右边为空或为最右
            if(flowerbed[i] == 0 && (i == 0 || flowerbed[i - 1] == 0) && (i == flowerbed.length - 1 ||  flowerbed[i + 1] == 0)){
                count++;
                flowerbed[i] = 1;
            }
        }
        return count >= n;
    }
}

细节

在 if 条件句中，要先写 i == 0 和 i == n - 1，防止角标越界。

665，非递减数列，easy

给你一个长度为 n 的整数数组，请你判断在最多改变 1 个元素的情况下，该数组能否变成一个非递减数列。

我们是这样定义一个非递减数列的：对于数组中所有的 i (0 <= i <= n-2)，总满足 nums[i] <= nums[i + 1]。

示例 1:

输入: nums = [4,2,3]
输出: true
解释: 你可以通过把第一个4变成1来使得它成为一个非递减数列。

示例 2:

输入: nums = [4,2,1]
输出: false
解释: 你不能在只改变一个元素的情况下将其变为非递减数列。

题解

当 nums 两个相邻元素不满足非递减时，造成了“下降”情况，可以修改为

nums[i] = nums[i + 1]
nums[i + 1] = nums[i]

贪心的思路，让 nums[i + 1] 尽可能的小，使后面更容易非递减。

但是采用上面哪一种需要小心，对不同的数组采取不同的处理方法。

如：

[1,2,3,1] 当 i 遍历到 3 时，发现比后面元素大，但如果采用第一种，将不满足非递减的条件，需要采用第二种。得到普遍规律为：nums[i + 1] < nums[i - 1] 时，使 nums[i + 1] = nums[i]。
[1,2,3,2] 当 i 遍历到 3 时，发现比后面元素大，贪心原则将当前元素改为左边元素值。得到普遍规律为：nums[i + 1] ≥ nums[i - 1] 时，使 nums[i] = nums[i + 1]。
特殊情况为：i == 0 且 nums[i] > nums[i + 1]，只能修改为右边元素值 nums[i] = nums[i + 1]。

在遍历过程中如果下降次数超过 1 次，则返回true，不用继续判断了。

代码

class Solution {
    public boolean checkPossibility(int[] nums) {
        int n = nums.length;
        if(n == 1) return true;
        int down = 0;//下降次数
        for(int i = 0; i < n - 1; i++){
            if(nums[i] > nums[i + 1]){
                down++;
                if(down > 1) return false;
                //[4,2,3]
                if(i == 0) nums[i] = nums[i + 1];
                //[1,3,2,4]
                else if(i >= 1 && nums[i + 1] >= nums[i - 1])
                    nums[i] = nums[i + 1];
                //[1,3,2,2]
                else if(i >= 1 && nums[i + 1] < nums[i - 1])
                    nums[i + 1] = nums[i];
            }
        }
        return true;
    }
}

53，最大子序和，easy

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

示例:

输入: [-2,1,-3,4,-1,2,1,-5,4]
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。

题解

贪心思想主要体现在当前元素加入前的 curSum 为负时，应将 curSum 舍弃，重新计算。

代码

class Solution {
    public int maxSubArray(int[] nums) {
        if(nums.length == 0 || nums == null) return 0;
        int res = nums[0];
        int curSum = nums[0];
        for(int i = 1; i < nums.length; i++){
            curSum += nums[i];
            //同时获取当前最大和
            maxSum = Math.max(maxSum, curSum);
            //只要正Sum不要负的，如果为负则重新计数
            if(curSum < 0)
                curSum = 0;
        }
        return maxSum;
    }
}

------ 本文结束感谢您的阅读 ------