LeetCode刷题—动态规划（二）

发表于 2020-12-29 更新于 2021-01-11 分类于 LeetCode刷题

刷了一系列这类的题，真的感受到dp 深深的套路，那就看看什么套路来解此类题吧！

300，最长递增子序列，medium 673，最长递增子序列的个数，medium 435，无重叠区间，medium 646，最长数对链，medium 452，用最少数量的箭引爆气球，medium

最长递增子序列

最长递增子序列（Longest Increasing Subsequence，简写 LIS）是比较经典的一个问题，比较容易想到的是动态规划解法，时间复杂度 O(N^2)。注意「子序列」和「子串」这两个名词的区别，子串一定是连续的，而子序列不一定是连续的。

300，最长递增子序列，medium

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

示例 1：

输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。

示例 2：

输入：nums = [0,1,0,3,2,3]
输出：4

示例 3：

输入：nums = [7,7,7,7,7,7,7]
输出：1

提示：

1 <= nums.length <= 2500

-104 <= nums[i] <= 104

思路：
1. 子问题
  
  到 nums[i] 的最长递增子序列的长度为 \(dp[i]\)
2. 递推关系
  - base case
    
    dp 数组应全部初始化为1，因为子序列最少也要包含自己。
  - 状态转移方程
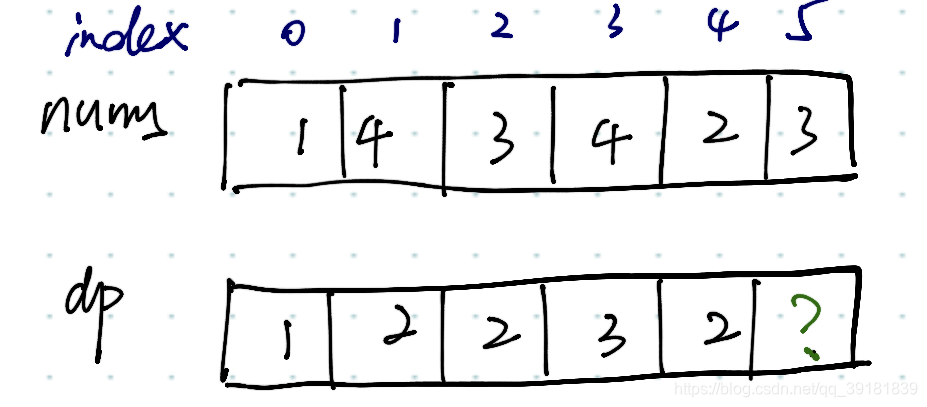
  在这里插入图片描述
  
  对于 \(dp[i]\)，比较 nums[i] 与前 i - 1 个元素，如果有比 nums[i] 小的元素 nums[j]，则 nums[i] 可以加入已形成的 \(dp[j]\) 之后，\(dp[i]\) 为与 \(dp[j] + 1\) 取最大值后的结果。
3. 返回值
  
  最终返回最大的 \(dp[i]\)，在第一次遍历数组得到 \(dp[0]\) ~ \(dp[i-1]\) 时，不断取最大值更新 res。

代码：

class Solution {
 public int lengthOfLIS(int[] nums) {
     int n = nums.length;
     int res = 1;

     int[] dp = new int[n];
     //base case
     Arrays.fill(dp, 1);
     //得到 dp[0] ~ dp[i-1]
     for(int i = 0; i < n; i++){
         //nums[i] 与前 i-1 个数字进行比较，得到 dp[i]
         for(int j = 0; j < i; j++){
             if(nums[j] < nums[i])
                 dp[i] = Math.max(dp[i], dp[j] + 1);
         }
         //在dp[0]~dp[n-1] 中找出最大值即为结果 
         res = Math.max(res, dp[i]);
     }        
     return res;
 }
 }

#### 673，最长递增子序列的个数，medium

给定一个未排序的整数数组，找到最长递增子序列的个数。

示例 1:

输入: [1,3,5,4,7]
输出: 2
解释: 有两个最长递增子序列，分别是 [1, 3, 4, 7] 和[1, 3, 5, 7]。

示例 2:

输入: [2,2,2,2,2]
输出: 5
解释: 最长递增子序列的长度是1，并且存在5个子序列的长度为1，因此输出5。

思路：
1. 子问题
  
  到 nums[i] 结尾，最长递增子序列的长度为 \(dp[i]\)，此外还需要一个数组 \(count[i]\) 来记录具有该长度的序列个数。
2. 递推关系
  - base case
    
    dp 数组应全部初始化为1，因为子序列最少也要包含自己。
    
    count 数组全部初始化为1，个数至少有一个。
  - 状态转移方程
    
    遍历[0...i]，再套一层[0....j]，其中 j＜i
    
    当 nums[j]＜nums[i]，说明可以形成最长递增序列，nums[i] 可以加入已形成的 \(dp[j]\) 之后。
    - 当 \(dp[j] + 1 > dp[i]\) 时，第一次出现此长度，\(dp[i] = dp[j] + 1\)，最长递增子序列的长度增加但个数不变，count[i] = count[j]
    - 当 \(dp[j] + 1 = dp[i]\) 时，在循环中已经出现过此长度，现在的组合方式 count[i] 加上 count[j] 并记录最大递增子序列长度
3. 返回值
  返回最大长度对应的种类数之和。
举例：
输入：[1,1,3,2]

代码：

class Solution {
  public int findNumberOfLIS(int[] nums) {
      if(nums.length == 0) return 0;
      int n = nums.length;
      int res = 0;
      int maxLength = 0;
      int[] dp = new int[n];
      int[] count = new int[n];
      Arrays.fill(dp, 1);
      Arrays.fill(count, 1);
      for(int i = 0; i < n; i++){
          for(int j = 0; j < i; j++){
              if(nums[j] < nums[i]){
                  if(dp[j] + 1 > dp[i]){
                      dp[i] = dp[j] + 1;
                      count[i] = count[j];
                  }
                  else if(dp[j] + 1 == dp[i]){
                      count[i] += count[j];
                  }   
              }
          }
          maxLength = Math.max(maxLength, dp[i]);
      }
      for(int i = 0; i < n; i++){
          if(dp[i] == maxLength){
              res += count[i];
          }
      
      return res;
  }
 }

一个小总结

上面两题思路是很像的，动态规划基于数学归纳法。
先得到第 i 位的最长递增子序列个数，最终结果（子序列的最大长度）应该是 dp 数组中的最大值。
而对 dp[i]，与前面的 i - 1 个数进行比较，加在前面的递增子序列之后，不断取最大值，得到 dp[i]。
第二题多增加了count 数组来记录最长子序列的个数，注意循环中的比较。

下面又是【最长递增子序列】的另一种题型，将上面题中的数组划分很多个小区间，如果能识别是同一种题就好解决了！

435，无重叠区间，medium

给定一个区间的集合，找到需要移除区间的最小数量，使剩余区间互不重叠。

注意:

可以认为区间的终点总是大于它的起点。
区间 [1,2] 和 [2,3] 的边界相互“接触”，但没有相互重叠。

示例 1:

输入: [ [1,2], [2,3], [3,4], [1,3] ]
输出: 1
解释: 移除 [1,3] 后，剩下的区间没有重叠。

示例 2:

输入: [ [1,2], [1,2], [1,2] ]
输出: 2
解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。

示例 3:

输入: [ [1,2], [2,3] ]
输出: 0
解释: 你不需要移除任何区间，因为它们已经是无重叠的了。

问题解析：

可以抽象成上面的问题：最长非严格递增子序列。题目要求可以接触但不可以重叠，即非严格递增。子序列长度改为区间个数，【删除区间的最小数量】即【保留区间的最大个数】。
思路：
1. 子问题
  
  到第 i 个区间，保留的最大区间数为 \(dp[i]\)。
2. 递推关系
  - base case
    
    dp 数组应全部初始化为1，因为最少也要保留一个区间。
  - 状态转移方程
    
    对于 \(dp[i]\)，前面 j = [0, i - 1] 个区间都有可能与它重叠（重叠即 j 的第 1 个元素 > i 的第 0 个元素），需要得到保留不重叠的区间的最大值。
    
    \(dp[i] = Math.max(dp[i], dp[j] + 1)\)
3. 返回值
  
  遍历过程中得到 ans 即保留不重叠的区间的最大值，最后返回 n - ans，即删除的最小区间个数。

代码：

  class Solution {
  	public int eraseOverlapIntervals(int[][] intervals) {
      	if(intervals.length == 0) return 0;
      	int n = intervals.length;
      	//对区间按起始数字进行排序
      	Arrays.sort(intervals, new Comparator<int[]>(){
          	@Override
          	public int compare(int[] o1, int[] o2) {
              	return o1[1]-o2[1];
          	}
      	});
      	//保留的最大区间个数
      	int ans = 1;
      	int[] dp = new int[n];
      	Arrays.fill(dp, 1);
      	for(int i = 1; i < n; i++){
          	for(int j = 0; j < i; j++){
              	//如果没有重叠（即右边的0元素大于等于左边的1元素），更新dp[i]
              	if(intervals[i][0] >= intervals[j][1])   
                  	dp[i] = Math.max(dp[i], dp[j] + 1);               
          	}
          	ans = Math.max(ans, dp[i]);
      	}
      	//删除的最小数量
      	return n - ans;
  	}
}

另一种：双指针

思路：

先对各个区间从小到大排序，左区间小的优先；相同情况下，右区间小的优先。

排序后两个指针分别指向相邻两个区间，不发生重叠继续比较下两个相邻区间；发生重叠则去除右元素较大的一个区间，这样较小的右区间才会尽可能减小与其他区间交集。

代码：

class Solution {
	public int eraseOverlapIntervals(int[][] intervals) {
    	Arrays.sort(intervals, new Comparator<int[]>() {
        	@Override
        	public int compare(int[] o1, int[] o2) {
            	if (o1[0] != o2[0]) {
                	return o1[0] - o2[0];
            	}else
                	return o1[1] - o2[1];
        	}
    	});
    	int count = 0;
    	//i指向待比较的左边区间，j指向待比较的右边区间
    	for (int i = 0, j = 1; i < intervals.length-1 && j<=intervals.length-1; i++,j++) {
        	//左边的1元素 > 右边的0元素，发生重叠，需要去除其中一个
        	if (intervals[i][1] > intervals[j][0]) {
            	//去除1元素较大的那个，如果右边区间的1元素较大，保留左边，i = i - 1，再次进入循环 i + 1，还在原位置;
            	//如果左边区间的1元素较大，保留右边，i = j - 1，再次进入循环 i + 1，i = j , j向后移
            	i = intervals[i][1] < intervals[j][1] ? i - 1: j - 1;
            	count++;
        	} 
        //不发生重叠
        	else {
            	i = j - 1;
        	}
    	}
    	return count;
	}
}

#### 646，最长数对链，medium

给出 n 个数对。在每一个数对中，第一个数字总是比第二个数字小。

现在，我们定义一种跟随关系，当且仅当 b < c 时，数对(c, d) 才可以跟在 (a, b) 后面。我们用这种形式来构造一个数对链。

给定一个数对集合，找出能够形成的最长数对链的长度。你不需要用到所有的数对，你可以以任何顺序选择其中的一些数对来构造。

示例：

输入：[[1,2], [2,3], [3,4]]
输出：2
解释：最长的数对链是 [1,2] -> [3,4]

问题说明：与上一题的区别在于数对之间不可以有相等数字，是严格递增的区间。返回的是最长数对区间个数。

代码：

class Solution {
  public int findLongestChain(int[][] pairs) {
      int n = pairs.length;   
       
      Arrays.sort(paris, new Comparator<int[]>(){
          @Override
          public int compare(int[] o1, int[] o2) {
              if (o1[0] != o2[0]) {
                  return o1[0] - o2[0];
              }else
                  return o1[1] - o2[1];
          }
      });
      int[] dp = new int[n];
      Arrays.fill(dp, 1);
      for(int i = 1; i < n; i++){
          for(int j = 0; j < i; j++){
              //不发生重叠, 更新 dp[i]
              if(pairs[i][0] > pairs[j][1]){
                  dp[i] = dp[j] + 1;
              }    
          }
      }
      //上面对pairs 进行了排序，dp数组递增，返回最后一个元素即最大值
      return dp[n - 1];
  }
}

#### 452，用最少数量的箭引爆气球，medium

在二维空间中有许多球形的气球。对于每个气球，提供的输入是水平方向上，气球直径的开始和结束坐标。由于它是水平的，所以纵坐标并不重要，因此只要知道开始和结束的横坐标就足够了。开始坐标总是小于结束坐标。

一支弓箭可以沿着 x 轴从不同点完全垂直地射出。在坐标 x 处射出一支箭，若有一个气球的直径的开始和结束坐标为 xstart，xend，且满足 xstart ≤ x ≤ xend，则该气球会被引爆。可以射出的弓箭的数量没有限制。弓箭一旦被射出之后，可以无限地前进。我们想找到使得所有气球全部被引爆，所需的弓箭的最小数量。

给你一个数组 points ，其中 points [i] = [xstart,xend] ，返回引爆所有气球所必须射出的最小弓箭数。

示例 1：

输入：points = [[10,16],[2,8],[1,6],[7,12]]
输出：2
解释：对于该样例，x = 6 可以射爆 [2,8],[1,6] 两个气球，以及 x = 11 射爆另外两个气球

示例 2：

输入：points = [[1,2],[3,4],[5,6],[7,8]]
输出：4

问题说明：\(dp[i]\) 表示到第 i 个区间的最小弓箭数。如果左边区间的1元素 >= 右边区间的0元素，说明有重叠，可以共用一个箭；如果左边区间的1元素 < 右边区间的0元素，没有重叠，\(dp[i] = dp[j] + 1\)。

代码：

class Solution {
  public int findMinArrowShots(int[][] points) {
      if(points.length == 0) return 0;

      int n = points.length;
      Arrays.sort(points, new Comparator<int[]>(){
          @Override
          public int compare(int[] o1, int[] o2) {
              if (o1[0] != o2[0]) {
                  return Integer.compare(o1[0], o2[0]);
              }else
                  return Integer.compare(o1[1], o2[1]);
          }
      });
      int[] dp = new int[n];
      Arrays.fill(dp, 1);
      for(int i = 1; i < n; i++){    
          for(int j = 0; j <= i - 1; j++){
              //如果区间不重叠（左边的1元素 < 右边的0元素），dp[j] + 1
              if(points[i][0] > points[j][1])
                  dp[i] = dp[j] + 1;
          }      
      }
      return dp[n - 1];
  }
}

注意：排序时，如果使用 o1[0]-o2[0] 、 o1[1]-o2[1] 在 [[-2147483646,-2147483645],[2147483646,2147483647]] 测试用例时会导致整形溢出。

一个小总结

这里动态规划的解法并不高效，只是为了讲解整体思路。
上面几题都是先对区间排序，再根据题意看是否重叠更新dp[i]。

继续刷题！继续更新！

------ 本文结束感谢您的阅读 ------