LeetCode刷题—重建二叉树

发表于 2020-12-21 更新于 2021-01-31 分类于 LeetCode刷题

LeetCode中有三道很类似的题，思路也大同小异，故作一总结。

105，从前序与中序遍历序列构造二叉树，medium 106，根据中序和后序遍历构造二叉树，medium 889，根据前序和后序遍历构造二叉树，medium

这三道题都是给出两种遍历方式，由其遍历顺序可发现规律来重建此二叉树。下面详解105题，后两题思路稍作改变，比较好懂了。

105，从前序与中序遍历序列构造二叉树，medium

根据一棵树的前序遍历与中序遍历构造二叉树。

注意: 你可以假设树中没有重复的元素。

例如，给出

前序遍历 preorder = [3,9,20,15,7] 中序遍历 inorder = [9,3,15,20,7] 返回如下的二叉树：

方法一：分治思想 + HashMap

前序遍历：根-左-右。

中序遍历：左-根-右。

以题目示例为例：
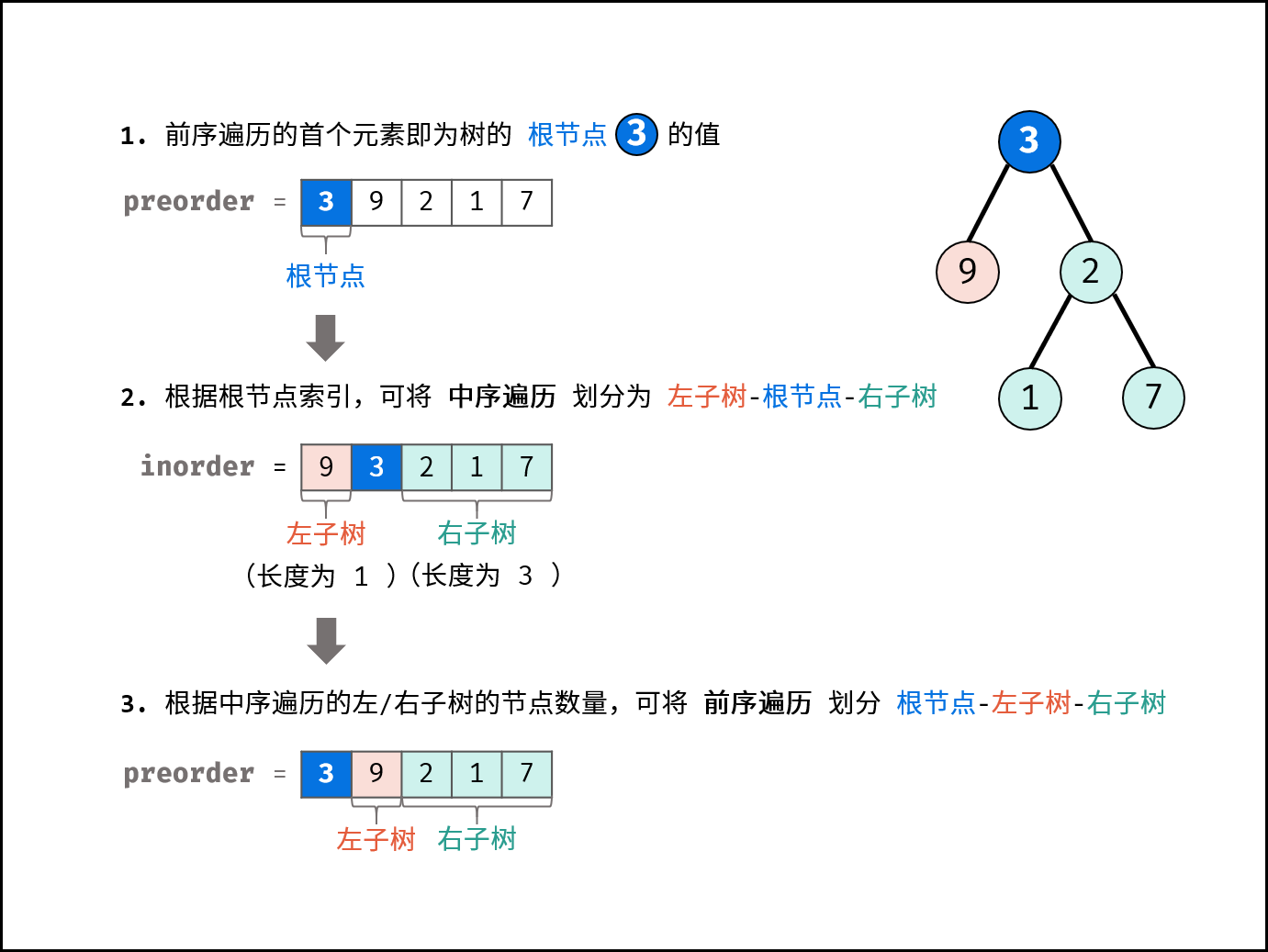
- 前序遍历划分 [ 3 | 9 | 20 15 7 ]
- 中序遍历划分 [ 9 | 3 | 15 20 7 ]
则前序遍历的首个元素为 根节点的值，在中序遍历数组中找到 根节点所在索引，其左边的元素为根节点的左子树，右边的元素为根节点的右子树。
以上子树的递推性质是 分治算法 的体现，考虑通过递归对所有子树进行划分。

辅助函数 build，参数为：前序遍历的起点索引 preL，结束索引 preR，中序遍历的起点索引 inL，结束索引 inR。

通过上面所述找到 root 在中序遍历的索引，递归其左边元素和右边元素，分别赋给 root 的左子树和右子树。递归出口为 preL > preR || inL > inR，表示越过叶子节点，此时返回null。
- 其中找到 root 在中序遍历的索引一种简单的方法是直接扫描整个中序遍历的结果并找出根节点，但这样做的时间复杂度较高。我们可以考虑使用 HashMap 快速地定位根节点。对于哈希映射中的每个键值对，键表示一个元素（节点的值），值表示其在中序遍历中的索引。
- 确定 preL、preR、inL、inR 需要解方程
  
  左子树在前序遍历中的起点索引：preL + 1
  
  左子树在前序遍历中的结束索引：x
```
 x 满足 x - (preL + 1) = rootIndex - 1 - intL=>  x = rootIndex - intL + preL
```
  左子树在中序遍历中的起点索引：intL
  
  左子树在中序遍历中的结束索引：rootIndex - 1
  
  右子树在前序遍历中的起点索引：x + 1
  
  右子树在前序遍历中的结束索引：preR
  
  右子树在中序遍历中的起点索引：rootIndex + 1
  
  右子树在中序遍历中的结束索引：inR

代码：

class Solution {
  private Map<Integer, Integer> map;
  private int[] preorder;
  public TreeNode buildTree(int[] preorder, int[] inorder) {
      this.preorder = preorder;
      map = new HashMap<>();
      //将中序遍历数组的元素和其索引存入map键值对
      for(int i = 0; i < inorder.length; i++){
          map.put(inorder[i], i);
      }
      return build(0, preorder.length - 1, 0, inorder.length - 1);
  }
  //前序遍历:preL起始索引，preR结束索引；中序遍历：inL起始索引，inR结束索引
  public TreeNode build(int preL, int preR, int inL, int inR){
      if(preL > preR || inL > inR) return null;
      //将前序遍历首个元素设为根节点
      int rootVal = preorder[preL];
      TreeNode root = new TreeNode(rootVal);
      //找到中序遍历中root的索引
      int rootIndex = map.get(rootVal);
      //递归调用中序遍历root左右部分形成root的左右子树
      root.left = build(preL + 1, rootIndex - inL + preL, inL, rootIndex - 1);
      root.right = build(rootIndex - inL + preL + 1, preR, rootIndex + 1, inR);
      return root;
  }
}

##### 方法二

和上面总体思想一样，但不借助 HashMap 来定位 root 在中序遍历数组的索引，而是用 List 的 indexOf 来定位，用 subList 确定左右子树的范围。

代码：

class Solution {

  public TreeNode buildTree(int[] preorder, int[] inorder) {
      List<Integer> prelist = new ArrayList<>();
      List<Integer> inlist = new ArrayList<>();
      //将int数组转为List
      for(int i = 0; i < preorder.length; i++){
          prelist.add(preorder[i]);
          inlist.add(inorder[i]);
      }
      return build(prelist, inlist);
  }
  public TreeNode build(List<Integer> prelist, List<Integer> inlist){
      if(inlist.isEmpty()) return null;
      //前序集合的首个元素为根节点
      int rootVal = prelist.remove(0);
      TreeNode root = new TreeNode(rootVal);
      //找到根节点在中序的索引
      int index = inlist.indexOf(rootVal);
      //新的左右两边
      root.left = build(prelist, inlist.subList(0, index));
      root.right = build(prelist, inlist.subList(index + 1, inlist.size()));
      
      return root;
  }
}

先把数组转化为list集合，然后在list集合中进行截取，这样效率明显不是很高。 #### 106，根据中序和后序遍历构造二叉树，medium 根据一棵树的中序遍历与后序遍历构造二叉树。

注意: 你可以假设树中没有重复的元素。

例如，给出

中序遍历 inorder = [9,3,15,20,7] 后序遍历 postorder = [9,15,7,20,3] 返回如下的二叉树：

思路：和上一题的思路基本一致，由中序遍历的规律（root 左部分为左子树，右部分为右子树），后序遍历的根节点为最后的节点。

代码：

class Solution {
  private Map<Integer, Integer> map;
  private int[] postorder;
  public TreeNode buildTree(int[] inorder, int[] postorder) {
      this.postorder = postorder;
      map = new HashMap<>();
      for(int i = 0; i < inorder.length; i++){
          map.put(inorder[i], i);
      }
      return build(0, inorder.length - 1, 0, postorder.length - 1);
  }
  public TreeNode build(int inL, int inR, int postL, int postR){
      if(inL > inR || postL > postR) return null;
      //在后序数组中找到根节点root
      int rootVal = postorder[postR];
      TreeNode root = new TreeNode(rootVal);
      //中序中root的索引
      int rootIndex = map.get(rootVal);
      root.left = build(inL, rootIndex - 1, postL, postL + rootIndex - 1 - inL);
      root.right = build(rootIndex + 1, inR, postL + rootIndex - inL, postR - 1);
      return root;
  }
}

#### 889，根据前序和后序遍历构造二叉树，medium 返回与给定的前序和后序遍历匹配的任何二叉树。

pre 和 post 遍历中的值是不同的正整数。

示例：

输入：pre = [1,2,4,5,3,6,7], post = [4,5,2,6,7,3,1] 输出：[1,2,3,4,5,6,7]

思路：还是按照之前的思路，找到根节点（即前序遍历的第一个元素或后序遍历的最后一个元素），但前序和后序不像中序的根作为分隔点，所以需要再找左子树的根在后序遍历数组的索引，依次来确定左右子树的长度。

代码：

class Solution {
  Map<Integer,Integer> map;
  private int[] post;
  private int[] pre;
  public TreeNode constructFromPrePost(int[] pre, int[] post) {
      this.post = post;
      this.pre = pre;
      map = new HashMap<>();
      for(int i = 0; i < post.length; i++){
          map.put(post[i], i);
      }
      return build(0, pre.length - 1, 0,  post.length - 1);
  }
  public TreeNode build(int preL, int preR, int postL, int postR){
      if(preL > preR || postL > postR) return null;
      //不加这步，下面int leftRoot = pre[preL + 1];会出现角标越界
      if(preL == preR) return new TreeNode(pre[preL]);

      //根的索引即前序第一个元素和后序最后一个元素
      TreeNode root = new TreeNode(post[postR]);
      //下面是为了确定左子树在数组中的长度
      //左子树根节点
      int leftRoot = pre[preL + 1];
      //左子树根节点在后序的索引
      int leftRootIndex = map.get(leftRoot);

      root.left = build(preL + 1, leftRootIndex - postL + preL + 1, postL, leftRootIndex);
      root.right = build(leftRootIndex - postL + preL + 2, preR, leftRootIndex + 1, postR - 1);
      return root;
  }
}

#### 总结

三个题中前序 + 中序和后序 + 中序，都利用中序的根左边部分是左子树，右边部分是右子树。所以先建立根节点，并找出根节点在中序遍历数组的索引，就可以利用此规律重建二叉树。
只有前序 + 后序时，无法利用中序遍历的规律，则需要再找出左子树的根节点，来确定左、右子树的长度。
用 HashMap 来以空间换时间，快速定位。
注意三题都不能有重复数字，才能用上面方法。

------ 本文结束感谢您的阅读 ------