LeetCode刷题—树的最近公共祖先
针对下面两题作出解答与总结： 235，二叉搜索树的最近公共祖先，easy 236，二叉树的最近公共祖先，medium
前序
最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”
p、q两节点一定在此树上，有两种情况： 1. p、q 在一个节点两侧，此节点即为p、q的公共祖先，如下图中 2 为p = 7、q = 4 的最近公共祖先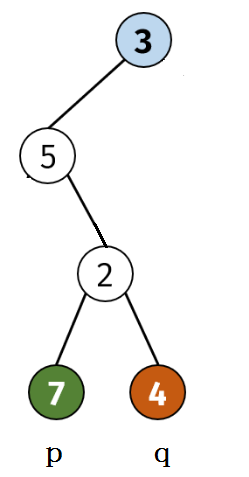 
2. p 或 q为最近公共祖先，如下图中 p 即为最近公共祖先 
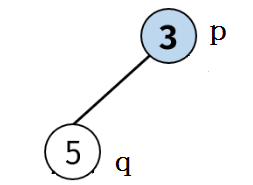### 235，二叉搜索树的最近公共祖先，easy 给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。 例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
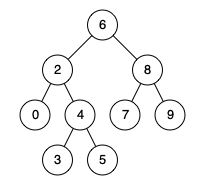
示例 1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8 |
示例 2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4 |
说明:
所有节点的值都是唯一的。 p、q 为不同节点且均存在于给定的二叉搜索树中。
方法一：递归。
思路：利用BST树左大右小的规律，p、q的位置有如下三种情况：
- 在root的一左一右：返回root
- 都在root左子树：递归root.left
- 都在root右子树：递归root.right
代码：
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root == null) return null;
if(p.val == root.val || q.val == root.val) return root;
if(p.val < root.val && q.val > root.val || p.val > root.val && q.val < root.val) return root;
if(p.val < root.val && q.val < root.val) return lowestCommonAncestor(root.left, p , q);
if(p.val > root.val && q.val > root.val) return lowestCommonAncestor(root.right, p , q);
return null;
}
}简洁版：
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
//两个差的乘积<=0，p、q分布在root两侧,返回root
if(p.val - root.val)*(q.val - root.val) <= 0){
return root;
}
return p.val < root.val ?lowestCommonAncestor(root.left,p,q) : lowestCommonAncestor(root.right,p,q);
}
}
方法二：迭代。
- 思路：p，q与root可能有三种关系。①p，q都在root的左子树 ②.p，q都在root的右子树 ③.p，q在root的一左一右。
- 通过p.val，q.val与root.val的差的乘积来判断。
- 如果大于0，说明①或②，则在root的左或右不断向下找，直到乘积为负返回此时根节点。
- 如果小于0，说明③，返回root。
- 代码：
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(p.val == root.val || q.val == root.val) return root;
//更新root直到找到p、q为两侧时的root
while(root != null){
if(p.val < root.val && q.val < root.val)
root = root.left;
else if(p.val > root.val && q.val > root.val)
root = root.right;
else break;
}
return root;
}
}
236，二叉树的最近公共祖先，medium
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
例如，给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]
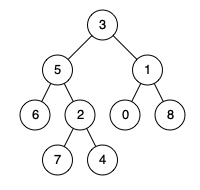
示例 1:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 |
示例 2:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 |
说明:
所有节点的值都是唯一的。 p、q 为不同节点且均存在于给定的二叉树中。
方法：递归回溯。
思路：二叉树没有什么特点 ，只能考虑先知道左右子树的情况，然后决定向上返回什么。因此采用「后序遍历」的思想。通过递归对二叉树进行后序遍历，当遇到节点 p 或 q 时返回。从底至顶回溯，当节点 p,q 在节点 root 的异侧时，节点 root 即为最近公共祖先，则向上返回 root 。
递归出口：
- root递归到叶子节点，返回 null
- 当 root 等于 p 或 q，返回 root
递归体：
递归左子节点和右子节点
TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
// 两种情况的 base case
if (root == null) return null;
if (root == p || root == q) return root;
TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q);
}回溯的结果有三种情况：
以下面为例，
（1）. 当 left和 right 同时不为空 ：说明 p,q 分列在 root 的 异侧 （分别在 左 / 右子树），因此 root为最近公共祖先，返回 root ；
（2）.当 left 和 right 有一为空，返回另一个值
left 为空，right 不为空，具体可分为两种情况：
- p,q 其中一个在 root 的 右子树 中，此时 right 指向 p（假设为 p ，图中 p = 2， q 在 3 的右子树中）；
- p,q 两节点都在 root 的 右子树 中，此时的 right 指向 最近公共祖先节点 （图中 p = 7， q = 4，返回公共节点 right = 2）；
或 
（3）left ，right 都为空，返回null 
- 代码：
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root == null) return null;
if(root.val == p.val || root.val == q.val) return root;
//分别递归左右子树
TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q);
//回溯结果
// if(left == null && right == null) return null;
if(left != null && right != null) return root;
return left == null ? right : left;
}
}