LeetCode刷题—递归解决树
对于树,经常用的算法有递归,回溯,BFS,DFS等。下面是一些用递归算法来解的题: 104,二叉树的最大深度,easy
104,二叉树的最大深度,easy
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例: 给定二叉树 [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7返回它的最大深度 3 。
代码:
class Solution {
public int maxDepth(TreeNode root) {
if(root == null) return 0;
int leftDepth = maxDepth(root.left);
int rightDepth = maxDepth(root.right);
return leftDepth >= rightDepth ? leftDepth + 1 : rightDepth + 1;
}
}
110,平衡二叉树,easy
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
示例 1:

输入:root = [3,9,20,null,null,15,7] |
示例 2:
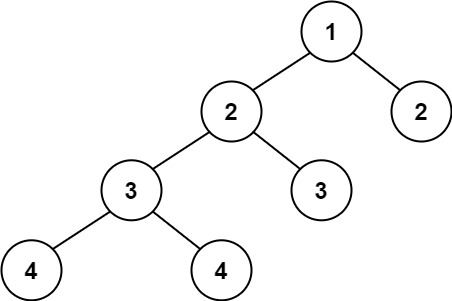
输入:root = [1,2,2,3,3,null,null,4,4] |
示例 3:
输入:root = [] |
思想:先判断root 为根节点的树是不是平衡二叉树,(即比较左右子树的高度差是否不超过1),再判断以root.left 和 root.right 为根节点的树是不是平衡二叉树。
代码:
class Solution {
public boolean isBalanced(TreeNode root) {
if(root == null) return true;
int l = depth(root.left);
int r = depth(root.right);
//判断当前根节点的树是否为平衡二叉树
if(Math.abs(l - r) > 1) return false;
else
return (isBalanced(root.left) && isBalanced(root.right));
}
//获取整棵树的高度
public int depth(TreeNode root){
if(root == null) return 0;
return Math.max(depth(root.left),depth(root.right)) + 1;
}
}
543,二叉树的直径,easy
给定一棵二叉树,你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。
示例 : 给定二叉树
1
/ \
2 3
/ \
4 5 返回 3, 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。
注意:两结点之间的路径长度是以它们之间边的数目表示。
方法:DFS递归。
思路:直径 = 任意两个结点路径长度中的最大值,可以看做树内的某一节点的左子树节点数l + 右子树节点数r - 1,所有节点的l + r - 1中的最大值即为直径。定义一个递归函数计算经过的左右子树的节点数l + r,函数返回给定节点为根的子树的深度。递归搜索每个节点并设一个全局变量 ans 记录 l + r 的最大值,最后返回 ans 即为树的直径。
代码:
class Solution {
int ans = 0;
public int diameterOfBinaryTree(TreeNode root) {
depth(root);
return ans;
}
//返回最大的 L+R
public int depth(TreeNode root){
if(root == null) return 0;
int l = depth(root.left);
int r = depth(root.right);
ans = Math.max(ans, l + r);//找到最大直径
return Math.max(l, r) + 1;//树的深度
}
}
226,翻转二叉树,easy
翻转一棵二叉树。
示例:
输入:
4
/ \
2 7
/ \ / \
1 3 6 9输出:
4
/ \
7 2
/ \ / \
9 6 3 1方法一:递归。
思路:分别对左右子树都进行翻转,再交换。
代码:
class Solution {
public TreeNode invertTree(TreeNode root) {
//递归
if(root == null) return null;
TreeNode leftTree = root.left;//保存原来的左子树
root.left = invertTree(root.right);
root.right = invertTree(leftTree);
return root;
}
}方法二:借助栈(DFS)。
思路:先将根节点压入栈。栈非空时,弹出栈顶节点,如果弹出节点的左右子节点有非空,将其压入栈,并进行交换,重复此过程直到栈空。
代码:
class Solution {
public TreeNode invertTree(TreeNode root) {
if(root == null) return null;
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while(!stack.isEmpty()){
TreeNode node = stack.pop();
if(node.left != null){
stack.push(node.left);
}
if(node.right != null){
stack.push(node.right);
}
TreeNode temp = node.right;
node.right = node.left;
node.left = temp;
}
return root;
}
}
617,合并二叉树,easy
给定两个二叉树,想象当你将它们中的一个覆盖到另一个上时,两个二叉树的一些节点便会重叠。
你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠,那么将他们的值相加作为节点合并后的新值,否则不为 NULL 的节点将直接作为新二叉树的节点。
示例 1:
输入: |
注意: 合并必须从两个树的根节点开始。
方法一:递归。(dfs)
思路:新建一棵树,如果原来两棵树的节点都存在,直接相加;如果有一个不存在,返回另一个节点。递归节点的左右子节点,作为新树的左右子树。
代码:
class Solution {
public TreeNode mergeTrees(TreeNode t1, TreeNode t2) {
if (t1 == null && t2 == null)
return null;
if(t1 == null || t2 == null){
return t1 == null ? t2 : t1;
}
TreeNode newTree = new TreeNode(t1.val + t2.val);
newTree.left = mergeTrees(t1.left,t2.left);
newTree.right = mergeTrees(t1.right,t2.right);
return newTree;
}
}
112,路径总和,easy
给定一个二叉树和一个目标和,判断该树中是否存在根节点到叶子节点的路径,这条路径上所有节点值相加等于目标和。
说明: 叶子节点是指没有子节点的节点。
示例: 给定如下二叉树,以及目标和 sum = 22,
5
/ \
4 8
/ / \
11 13 4
/ \ \
7 2 1返回 true, 因为存在目标和为 22 的根节点到叶子- 方法一:递归(dfs)
思路:以当前根节点为例,如果为null,返回false;如果为叶子节点,判断当前节点值是否与sum相等并返回;如果不是叶子节点,递归搜索左右子节点。
代码:
class Solution {
public boolean hasPathSum(TreeNode root, int sum) {
if(root == null) return false;
if(root.left == null && root.right == null) return root.val == sum;
return hasPathSum(root.left,sum - root.val) || hasPathSum(root.right, sum - root.val);
}
}
113,路径总和Ⅱ,midium
给定一个二叉树和一个目标和,找到所有从根节点到叶子节点路径总和等于给定目标和的路径。
说明: 叶子节点是指没有子节点的节点。
示例: 给定如下二叉树,以及目标和 sum = 22,
5
/ \
4 8
/ / \
11 13 4
/ \ / \
7 2 5 1返回:
[ |
方法:递归回溯(dfs)。
思路:
- 回溯条件:
- 节点为空— 如果当前节点为空,说明节点没有孩子,循着这条路径,已经找不到符合条件的路径。
- 节点为叶子节点— 如果当前节点是叶子节点并且它的值满足题目要求,则它所在的路径就是满足要求的。
- 回溯条件:
代码:
class Solution {
List<List<Integer>> res = new ArrayList<>();
public List<List<Integer>> pathSum(TreeNode root, int sum) {
dfs(root, sum, res, new ArrayList<>());
return res;
}
public void dfs(TreeNode root, int sum, List<List<Integer>> res, List<Integer> list){
if(root == null) return;
//把当前节点值加入到list中
list.add(root.val);
//叶子节点且此节点值=sum
if(root.left == null && root.right == null && root.val == sum) res.add(new ArrayList(list));
//还没到叶子节点,继续从左右节点向下找
dfs(root.left, sum - root.val, res, list);
dfs(root.right, sum - root.val, res, list);
//防止分支污染,遍历完当前节点的左子树、右子树,说明经过这个节点的路径已经被遍历完,因此要回溯到当前节点的父节点
list.remove(list.size() - 1);
}
}
572,另一个树的子树,easy
给定两个非空二叉树 s 和 t,检验 s 中是否包含和 t 具有相同结构和节点值的子树。s 的一个子树包括 s 的一个节点和这个节点的所有子孙。s 也可以看做它自身的一棵子树。
示例 1: 给定的树 s:
3
/ \
4 5
/ \
1 2 给定的树 t:
4 |
返回 true,因为 t 与 s 的一个子树拥有相同的结构和节点值。
示例 2: 给定的树 s:
3 |
给定的树 t:
4 |
返回 false。
方法:建立一个递归函数,判断两棵树是否相等。
代码:
class Solution {
public boolean isSubtree(TreeNode s, TreeNode t) {
//第二棵树为空,一定是子树
if(t == null) return true;
//第一棵树为空,没有子树
if(s == null) return false;
//递归比较t是否是s的左子树和右子树的一部分,或s与t是两棵相同的树
return isSubtree(s.left, t) || isSubtree(s.right, t) || isSameTree(s, t);
}
//判断两棵树是否相同
public boolean isSameTree(TreeNode s, TreeNode t){
if(s == null && t == null) return true;
//如果其中有一个节点为空或两节点值不相等时,返回false
if(s == null || t == null || s.val != t.val) return false;
//递归比较左子树和右子树是否相同
return isSameTree(s.left, t.left) && isSameTree(s.right, t.right);
}
}
101,对称二叉树,easy
给定一个二叉树,检查它是否是镜像对称的。
例如,二叉树 [1,2,2,3,4,4,3] 是对称的。
1
/ \
2 2
/ \ / \
3 4 4 3但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:
1
/ \
2 2
\ \
3 3方法一:递归。
思路:建立一个递归函数,移动两个指针遍历这棵树,判断根节点的左右子树是否对称。在主函数调用此递归函数,参数为根的左子节点和右子节点。
代码:
class Solution {
public boolean isSymmetric(TreeNode root) {
if(root == null) return true;
return check(root.left, root.right);
}
//用两个指针检查树是否对称
public boolean check(TreeNode p, TreeNode q){
if(p == null && q == null) return true;
if(p == null || q == null || p.val != q.val) return false;
return check(p.left, q.right) && check(p.right, q.left);
}
}
111,二叉树的最小深度,easy
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。
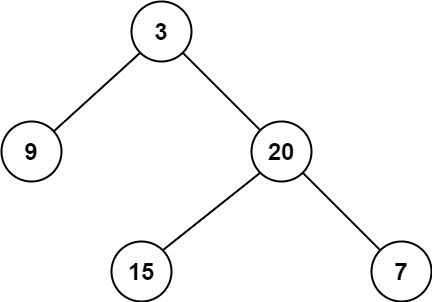
示例 1:
输入:root = [3,9,20,null,null,15,7] |
示例 2:
输入:root = [2,null,3,null,4,null,5,null,6] |
方法一:递归。
- 结束条件:当root为空,返回0
- 递归体:若左右子树皆空,返回1;若左子树和右子树有非空的,记录其最小路径,最后返回结果为最小路径 ➕ 1
代码:
class Solution {
public int minDepth(TreeNode root) {
if(root == null) return 0;
//1.当root的左右子树都为空
if(root.left == null && root.right == null) return 1;
int mindep = Integer.MAX_VALUE;
//2.root的左子树或右子树有不为空,计算其最小路径
if(root.left != null){
mindep = Math.min(minDepth(root.left), mindep);
}
if(root.right != null){
mindep = Math.min(minDepth(root.right), mindep);
}
//返回最小路径+1
return mindep + 1;
}
}错误原因:想法是dfs 来递归左右子树找它们的最小路径,然后取最小。但这样可能在 [2,null,3,null,4,null,5,null,6] 结构中不成立,因为root的左子树为空,所以要加一个判断。
404,左叶子之和,easy
计算给定二叉树的所有左叶子之和。
示例:
3
/ \
9 20
/ \
15 7在这个二叉树中,有两个左叶子,分别是 9 和 15,所以返回 24
方法一:递归dfs
思路:所有左叶子节点之和,需要遍历整棵树,采用dfs。
递归出口:节点为空或为叶子节点
递归条件:
- 如果左子树不为空,判断左子节点是否为叶子节点:若不是,递归调用左子节点
- 如果右子树为空,结果不变;若不为空,上面的结果+ 递归调用右子节点
- 否则左子树为空,右子树一定不为空,只需判断右子节点是不是叶子节点,若不是,递归调用右子节点
- 最后返回结果
- 如果左子树不为空,判断左子节点是否为叶子节点:若不是,递归调用左子节点
代码:
class Solution {
public int sumOfLeftLeaves(TreeNode root) {
if(root == null || isLeaf(root)) return 0;
return dfs(root);
}
public int dfs(TreeNode root){
if(root == null || isLeaf(root)) return 0;
int res = Integer.MAX_VALUE;
if(root.left != null){
res = isLeaf(root.left) ? root.left.val : dfs(root.left);
if(root.right != null)
res += isLeaf(root.right) ? 0 : dfs(root.right);
}
else{
res = isLeaf(root.right) ? 0 : dfs(root.right);
}
return res;
}
public boolean isLeaf(TreeNode node){
return node.left == null && node.right == null;
}
}更简洁的版本:
public int sumOfLeftLeaves(TreeNode root) {
if (root == null) return 0;
if (isLeaf(root.left)) return root.left.val + sumOfLeftLeaves(root.right);
return sumOfLeftLeaves(root.left) + sumOfLeftLeaves(root.right);
}
private boolean isLeaf(TreeNode node){
if (node == null) return false;
return node.left == null && node.right == null;
}另一题:一棵树所有左子节点的值
class Solution {
public int sumOfLeftLeaves(TreeNode root) {
if(root == null) return 0;
if(root.left == null && root.right == null) return 0;
int res = Integer.MAX_VALUE;
if(root.left != null && root.right == null){
res = sumOfLeftLeaves(root.left) + root.left.val;
}
if(root.left == null && root.right != null){
res = sumOfLeftLeaves(root.right);
}
if(root.left != null && root.right != null){
res = sumOfLeftLeaves(root.left) + root.left.val + sumOfLeftLeaves(root.right);
}
return res;
}
}
687,最长同值路径,medium
给定一个二叉树,找到最长的路径,这个路径中的每个节点具有相同值。 这条路径可以经过也可以不经过根节点。
注意:两个节点之间的路径长度由它们之间的边数表示。
示例 1:
输入:
5
/ \
4 5
/ \ \
1 1 5输出:
2 |
示例 2:
输入:
1
/ \
4 5
/ \ \
4 4 5输出:
2 |
方法一:递归。(dfs)
思路:
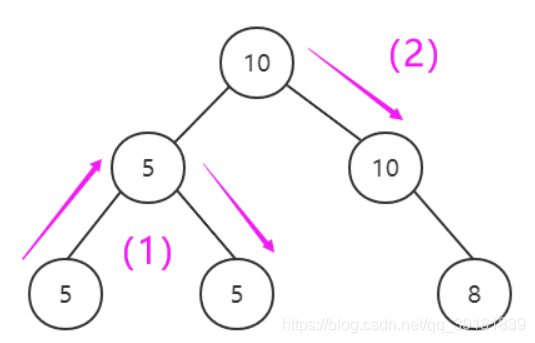
最长路径分为2种情况:
- 以root为起点,经过左子树或右子树,如(2)
- 不以root为起点,root为中间点,如(1)
辅助函数helper,计算以每一个节点为起点的最长同值路径maxLength,在过程中可以得到以root为根节点的树的最长同值路径ans。
代码:
class Solution {
int ans;
//以root为根节点的树的最长同值路径
public int longestUnivaluePath(TreeNode root) {
if(root == null) return 0;
helper(root);
return ans;
}
//以root为起点的最长同值路径
public int helper(TreeNode root){
if(root == null) return 0;
int maxLength = 0;
//以左、右子节点为起点的最长同值路径
int leftLength = helper(root.left);
int rightLength = helper(root.right);
//如果左、右子树都非空 且 root.val == root.left.val == root.right.val,更新ans
if(root.left != null && root.right != null && root.val == root.left.val && root.val == root.right.val){
ans = Math.max(ans, leftLength + rightLength + 2);
}
int leftPath = 0;
int rightPath = 0;
//如果左右子树有非空且子节点的值与root的值相等,以根节点为起点的最长同值路径为leftPath,rightPath中的最大值
if(root.left != null && root.left.val == root.val){
leftPath = leftLength + 1;
}
if(root.right != null && root.right.val == root.val){
rightPath = rightLength + 1;
}
//取左右子树的最长同值路径的最大值
maxLength = Math.max(leftPath,rightPath);
//更新ans
ans = Math.max(ans, maxLength);
return maxLength;
}
}简洁版:
private int path = 0;
public int longestUnivaluePath(TreeNode root) {
dfs(root);
return path;
}
private int dfs(TreeNode root){
if (root == null) return 0;
int left = dfs(root.left);
int right = dfs(root.right);
int leftPath = root.left != null && root.left.val == root.val ? left + 1 : 0;
int rightPath = root.right != null && root.right.val == root.val ? right + 1 : 0;
path = Math.max(path, leftPath + rightPath);
return Math.max(leftPath, rightPath);
}
671,二叉树中第二小的节点,easy
给定一个非空特殊的二叉树,每个节点都是正数,并且每个节点的子节点数量只能为 2 或 0。如果一个节点有两个子节点的话,那么该节点的值等于两个子节点中较小的一个。
更正式地说,root.val = min(root.left.val, root.right.val) 总成立。
给出这样的一个二叉树,你需要输出所有节点中的第二小的值。如果第二小的值不存在的话,输出 -1 。
示例 1:

输入:root = [2,2,5,null,null,5,7] |
示例 2:

输入:root = [2,2,2] |
题意解析:每个树的根节点的值都为这棵树所有节点最小的值,所有节点中第二小的值即只比根节点大的值。
方法一:递归。
- 递归出口:节点为空,返回 -1。
- 递归体:
- 左右子节点都为空,返回 -1。
- 根节点取的是左子节点的值,递归左子节点得到只比这个值大的值(或 -1,即此节点为叶子节点)
- 根节点取的是右子节点的值,递归右子节点得到只比这个值大的值(或 -1,即此节点为叶子节点)
- 结果:
- left 、right 如果都不为 -1,取最小值并返回
- left 不为 -1(right 为 -1),返回left
- 否则(left为 -1),返回right(-1 或 root.right.val或递归结果)
代码:
class Solution {
public int findSecondMinimumValue(TreeNode root) {
if(root == null) return -1;
if(root.left == null && root.right == null) return -1;
int left = root.left.val;
//如果左子节点是最小值,递归左子节点,得到以左子节点为根的树的第二小的值 或 -1
if(left == root.val){
left = findSecondMinimumValue(root.left);//-1 或 以root.left为根的树的第二小的值
}
int right = root.right.val;
//如果右子节点是最小值,递归右子节点,得到以右子节点为根的树的第二小的值 或 -1
if(right == root.val){
right = findSecondMinimumValue(root.right);//-1 或 以root.right为根的树的第二小的值
}
//如果两边的树递归结果都不为-1(都正常),返回它们的最小值,即在root为根的树中只比root.val大
if(left != -1 && right != -1) return Math.min(left,right);
//如果左子树正常,返回左子树
if(left != -1) return left;
//否则返回右子树递归值(-1 或 以root.right为根的树的第二小的值)
else return right;
}
}