递归与回溯
递归与回溯
一句话讲递归与回溯
递归:自己调用自己。本质就是找到前后的联系,找到递归的公式。
回溯:执行一次深度优先遍历(DFS),一条路走到底,走不通的时候,返回回来,继续执行,一直这样下去,直到回到起点。
递归
一般情况为:
if (终止条件) { |
例子:阶乘
阶乘
public int recursion(int n) {
//终止条件
if (n == 1)
return 1;
//调用自己
return n * recursion(n - 1);
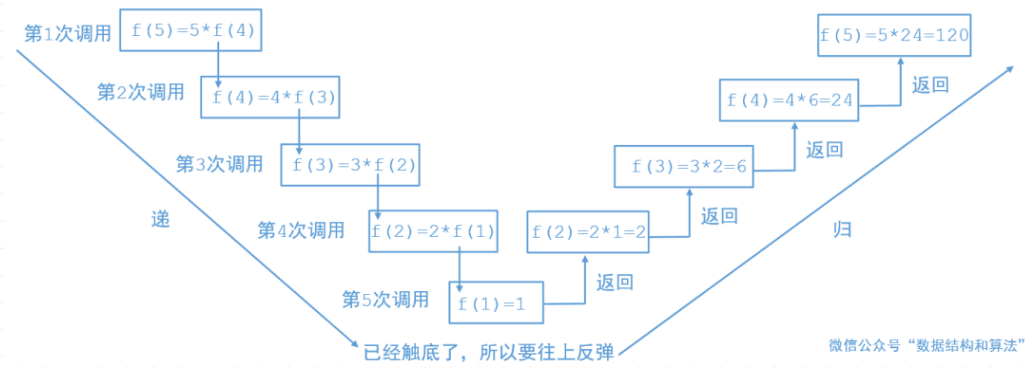
}递归过程:
求f(5)的时候,只需要求出f(4)即可,如果求f(4)我们要求出f(3)……,一层一层的调用,当n=1的时候,我们直接返回1,然后再一层一层的返回,直到返回f(5)为止。
一些较实际的情况:
if (终止条件) { |
例子:反转链表
反转链表
public static void reverseList(ListNode root) {
//(终止条件)
if (root == null)
return ;
//(递归调用)先打印下一个
reverseList(root.next);
//(逻辑处理)把后面的都打印完了在打印当前节点
System.out.print(root.val + " ");
}结果如下:
回溯
回溯的本质,其实是在递归基础上进行了改进
一般情况为:
if(不满足继续递归查找的条件,通常为界限判断) |
例子:矩阵中的路径(剑指Offer12)
判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。
示例:
输入:board = [ |
思路:回溯算法(DFS+剪枝)。遍历矩阵中所以字符,先朝一个方向搜索到底,再回溯至上个节点,再沿另一方向搜索,以此类推。在搜索中,遇到匹配不成功(如索引越界、此元素已访问、此矩阵元素和目标字符不同)的情况就立即返回。
代码实现
class Solution {
public boolean exist(char[][] board, String word) {
char[] words = word.toCharArray();
for(int i = 0; i < board.length; i++) {
for(int j = 0; j < board[0].length; j++) {
if(dfs(board, words, i, j, 0)) return true;
}
}
return false;
}
//回溯
boolean dfs(char[][] board, char[] word, int i, int j, int k) {
//边界条件(越界、与目标元素不同)
if(i >= board.length || i < 0 || j >= board[0].length || j < 0 || board[i][j] != word[k]) return false;
//全部匹配完成
if(k == word.length - 1) return true;
char temp = board[i][j];
board[i][j] = '\0';//将当前元素标记为'\0',不可再被访问
//递归上下左右
boolean res = dfs(board, word, i + 1, j, k + 1) || dfs(board, word, i - 1, j, k + 1) ||dfs(board, word, i, j + 1, k + 1) || dfs(board, word, i , j - 1, k + 1);
board[i][j] = temp;//恢复其本身值
//递归结果判断-回溯
return res;//上面4个方向,只要有一个能查找到,就返回true
}
}
例子:二叉搜索树的最近公共祖先(剑指Offer68-Ⅱ)
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
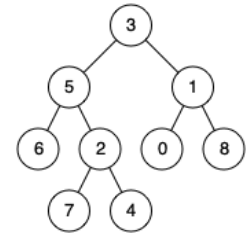
例如,给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]
示例 1:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 |
示例 2:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 |
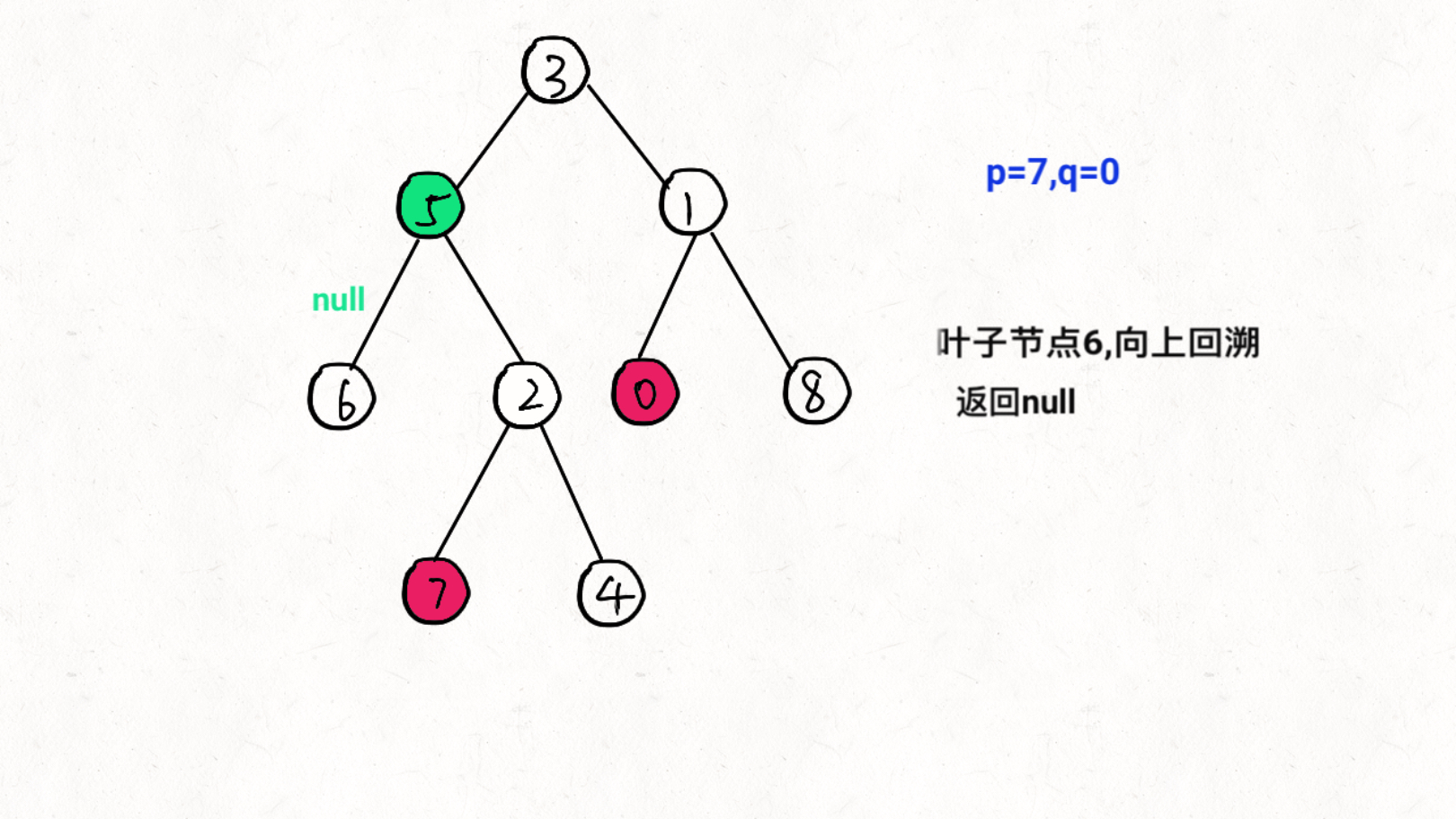
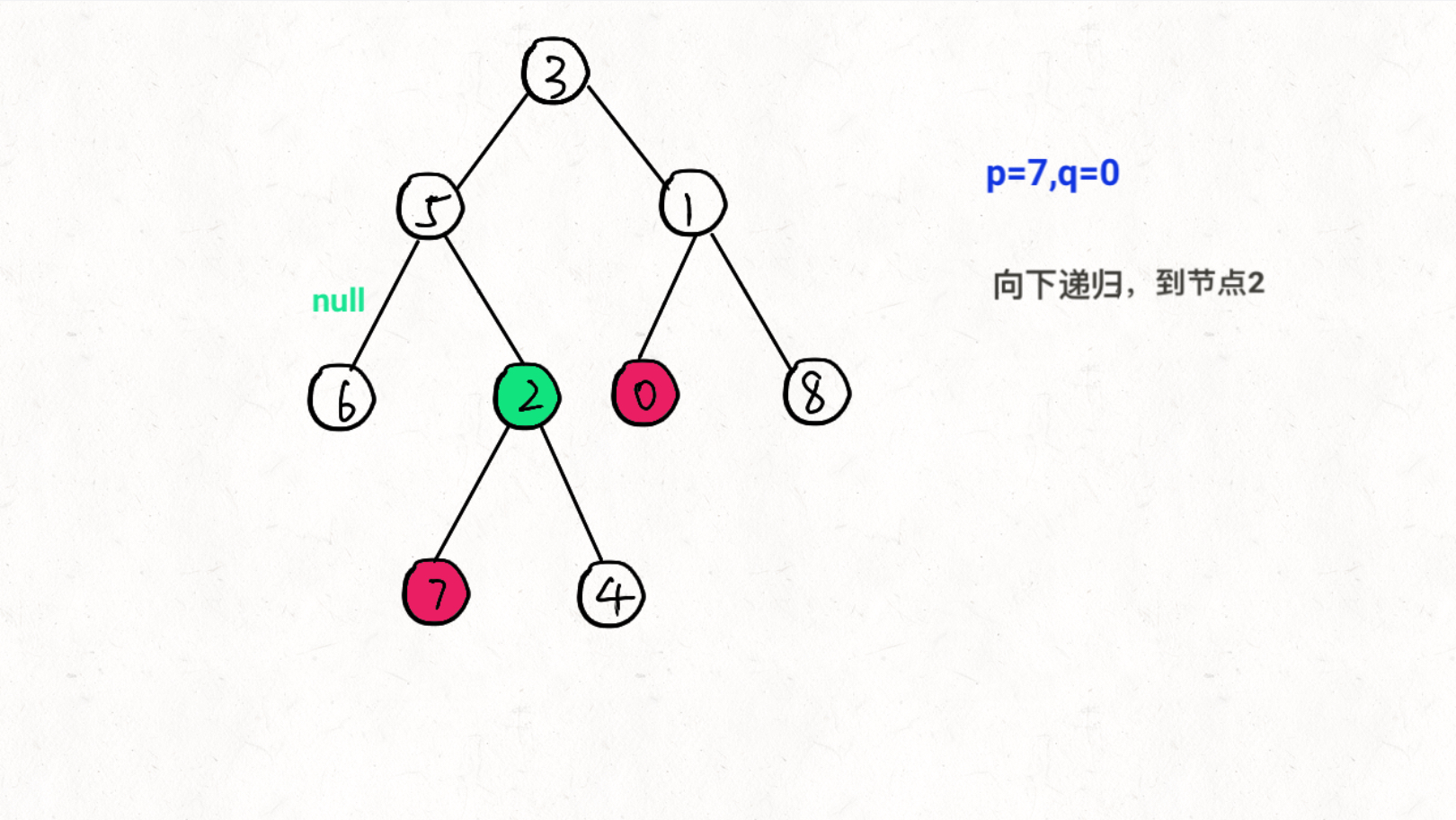
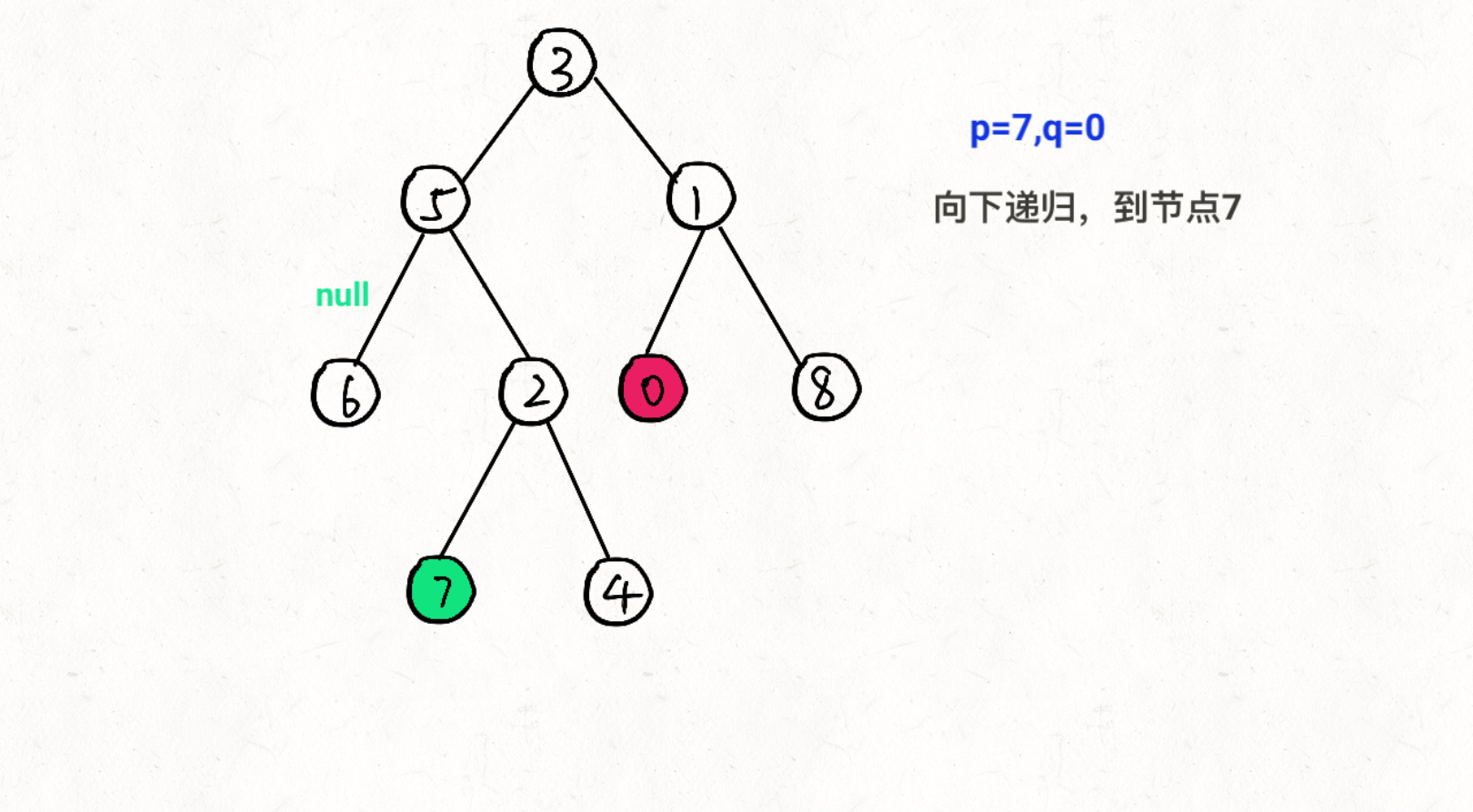
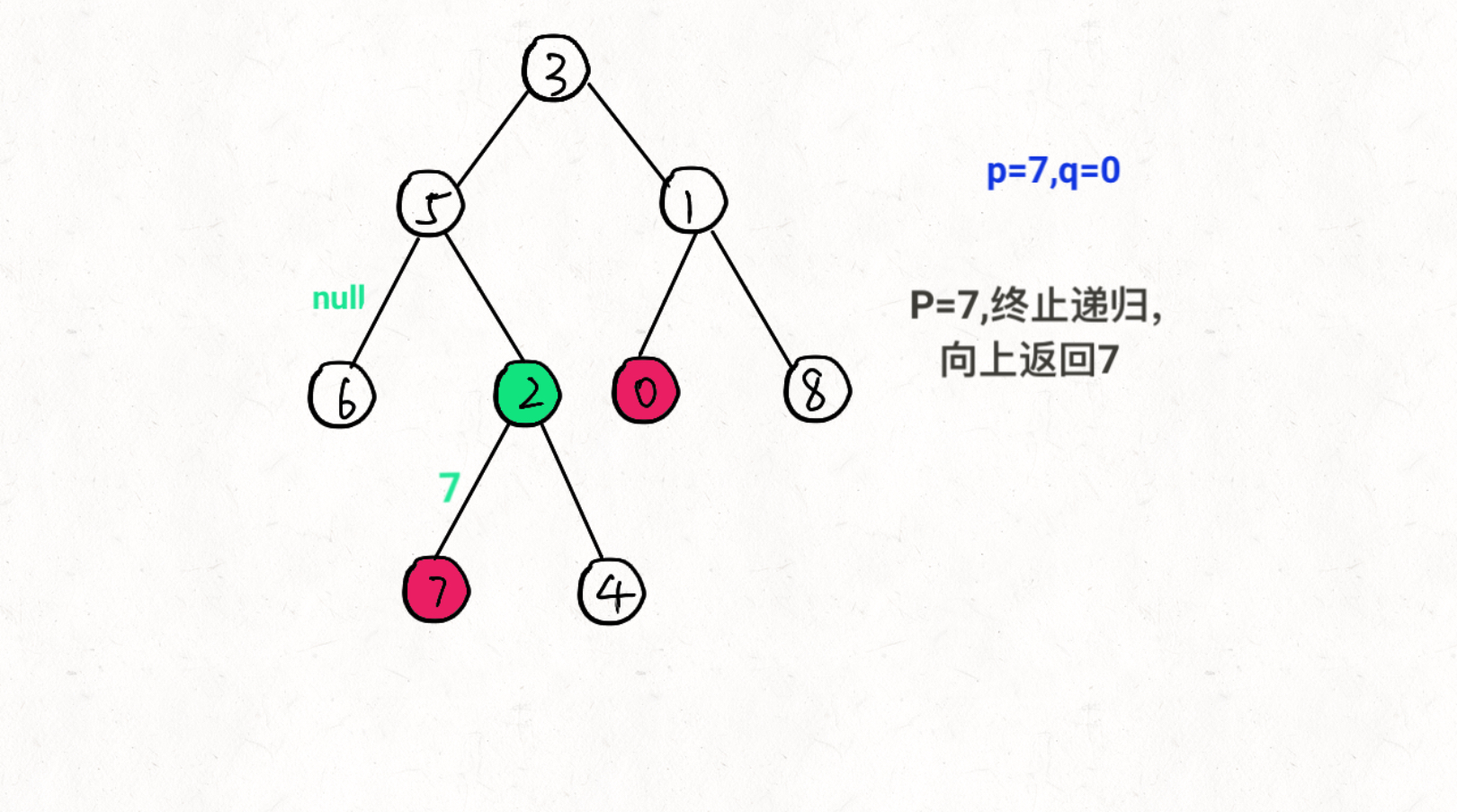
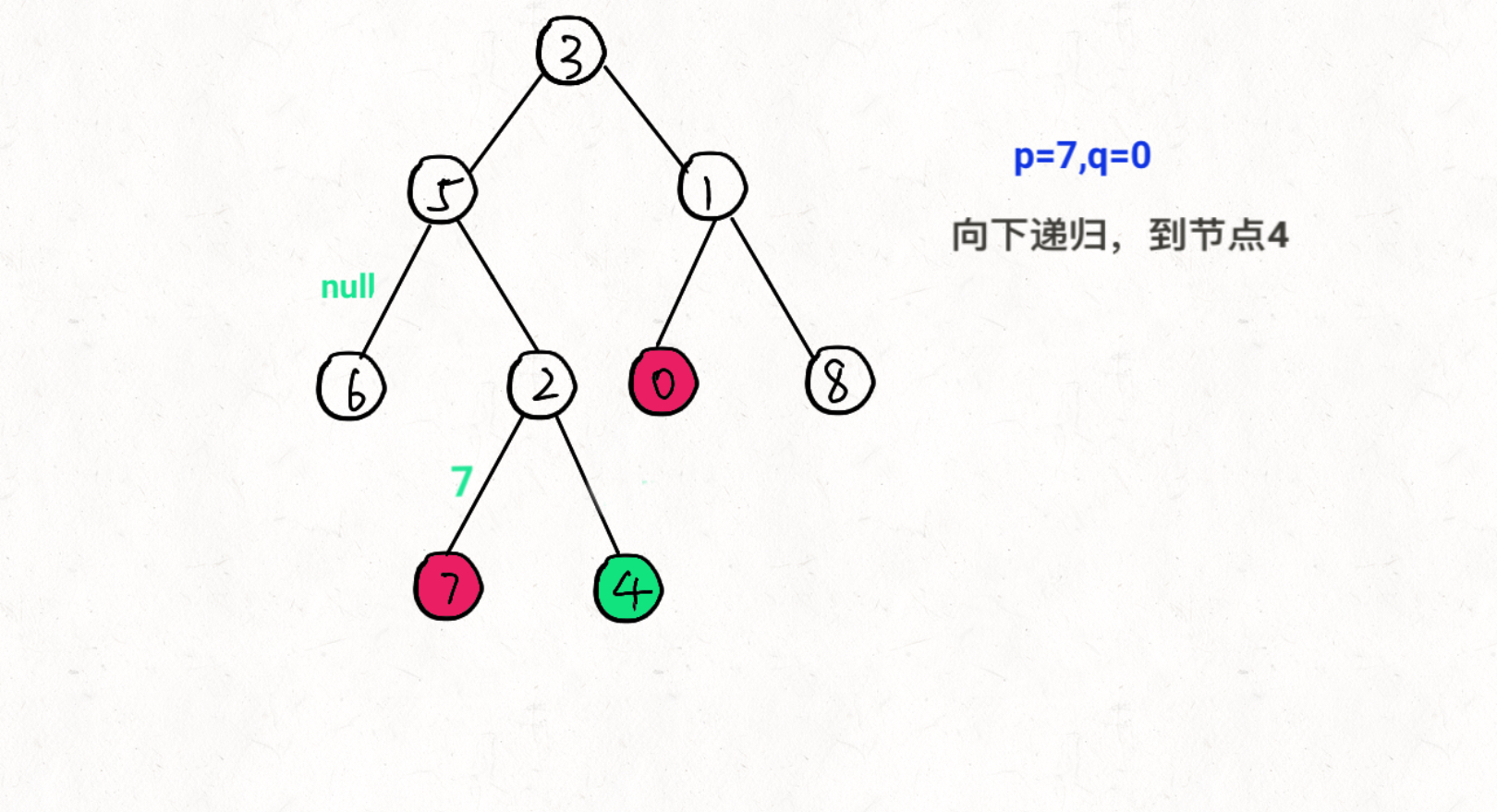
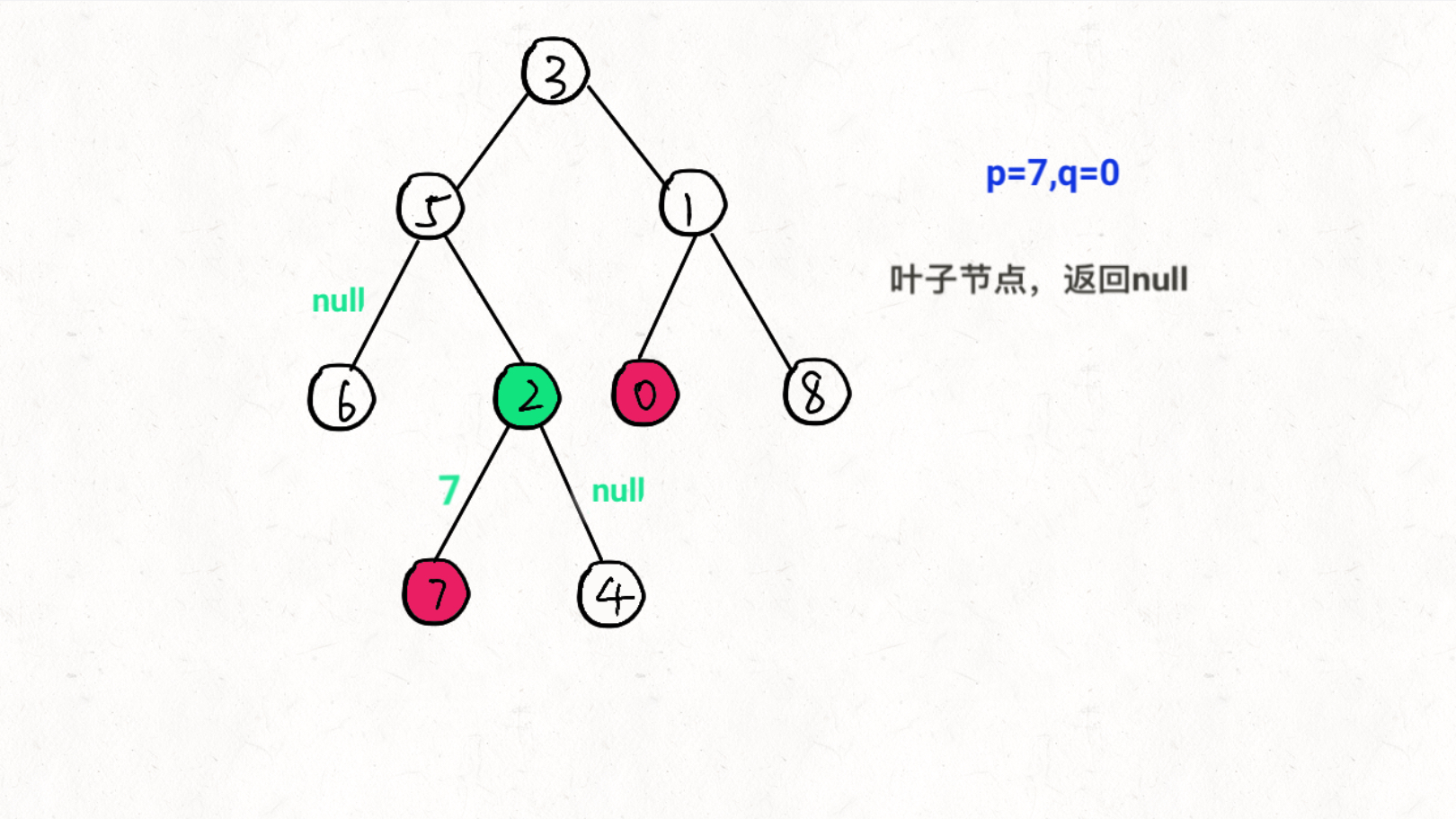
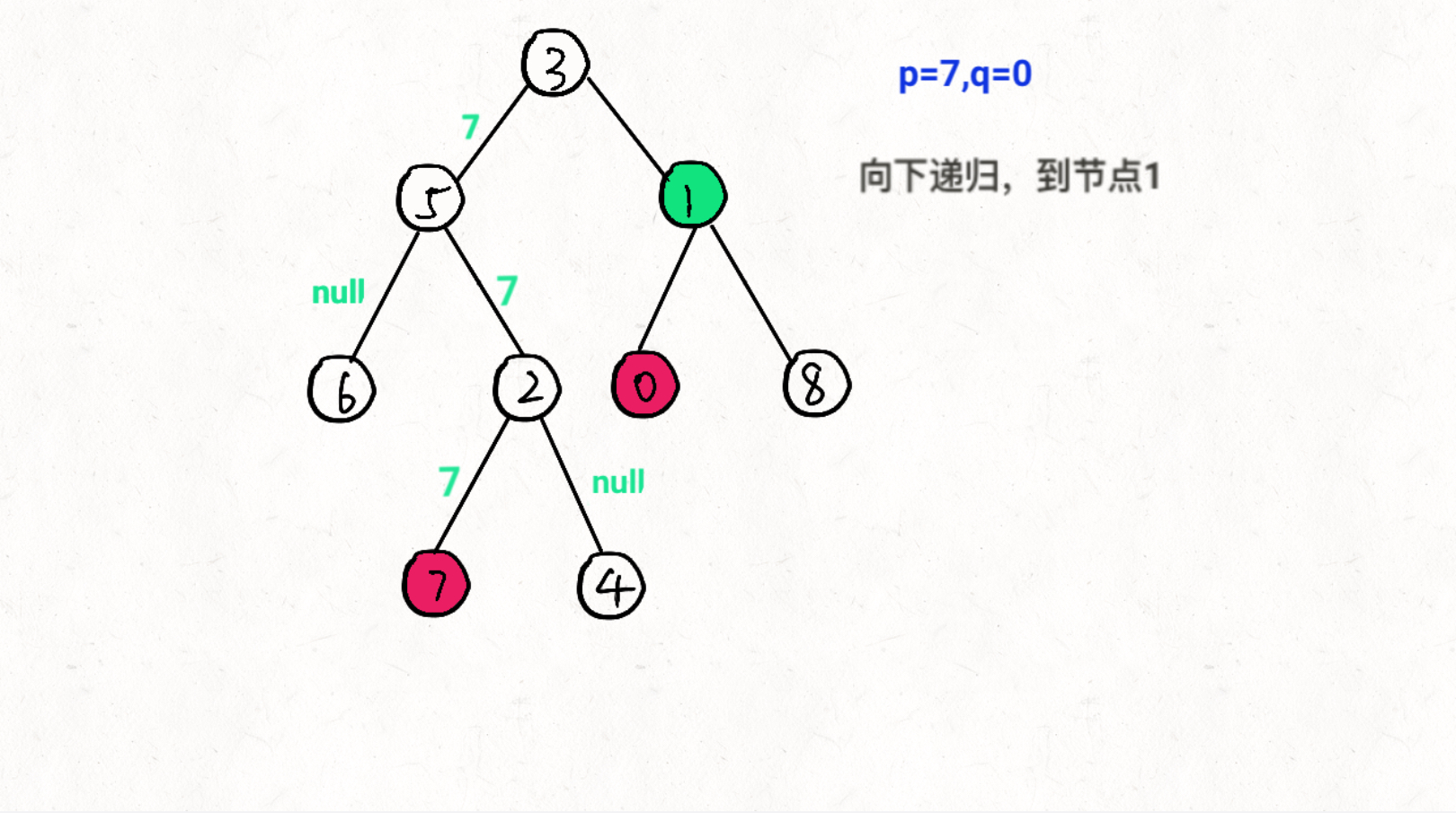
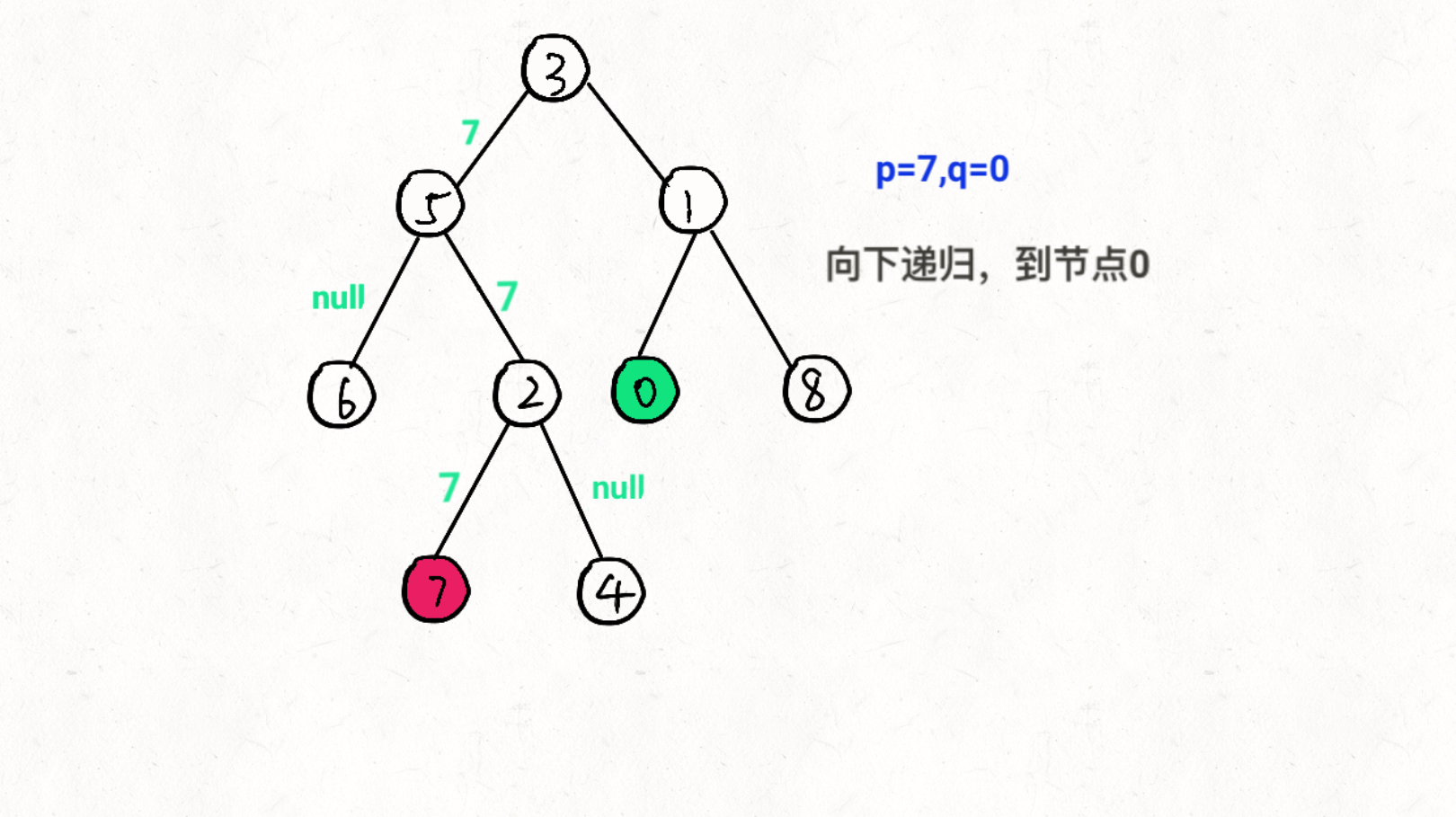
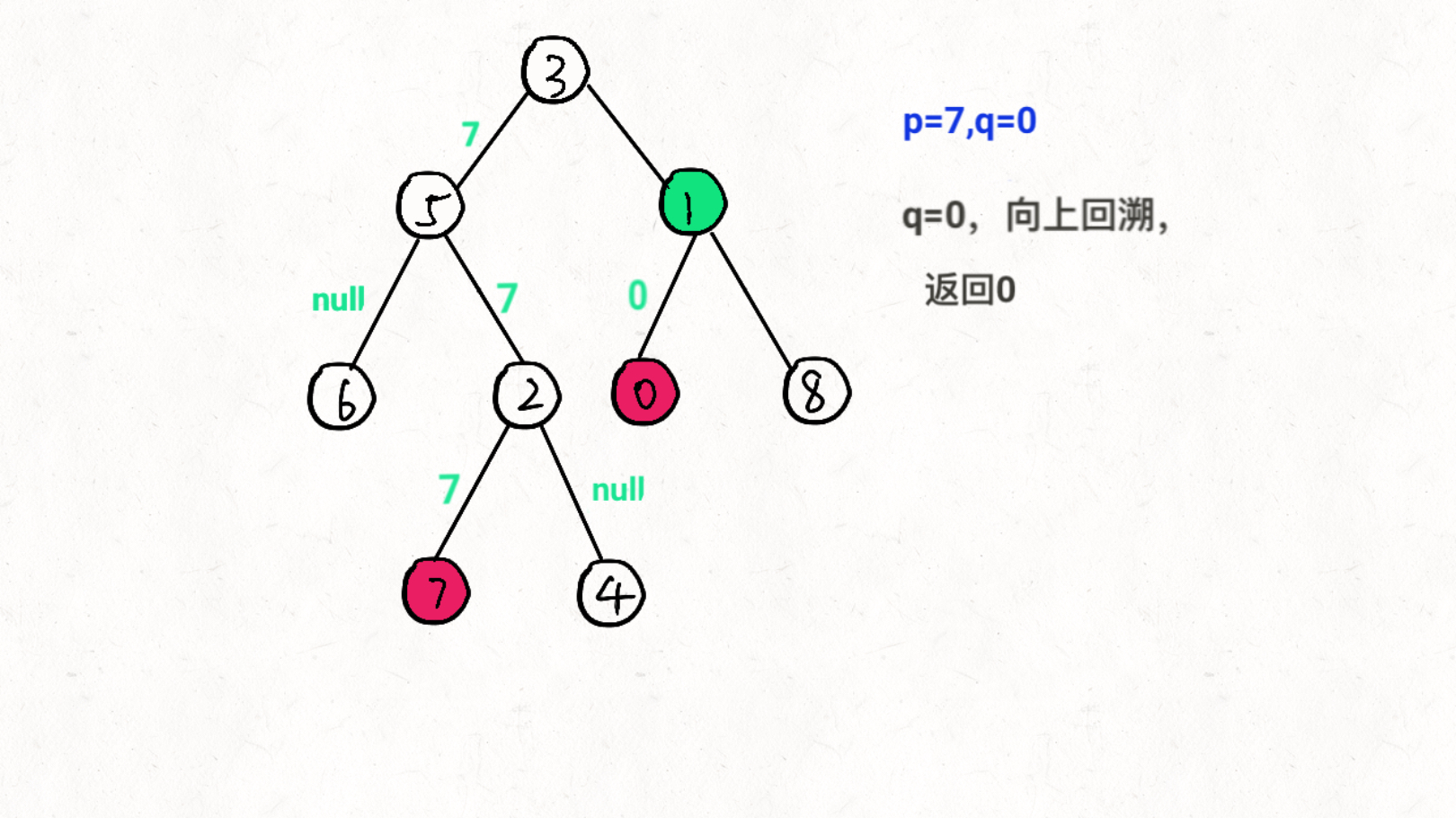
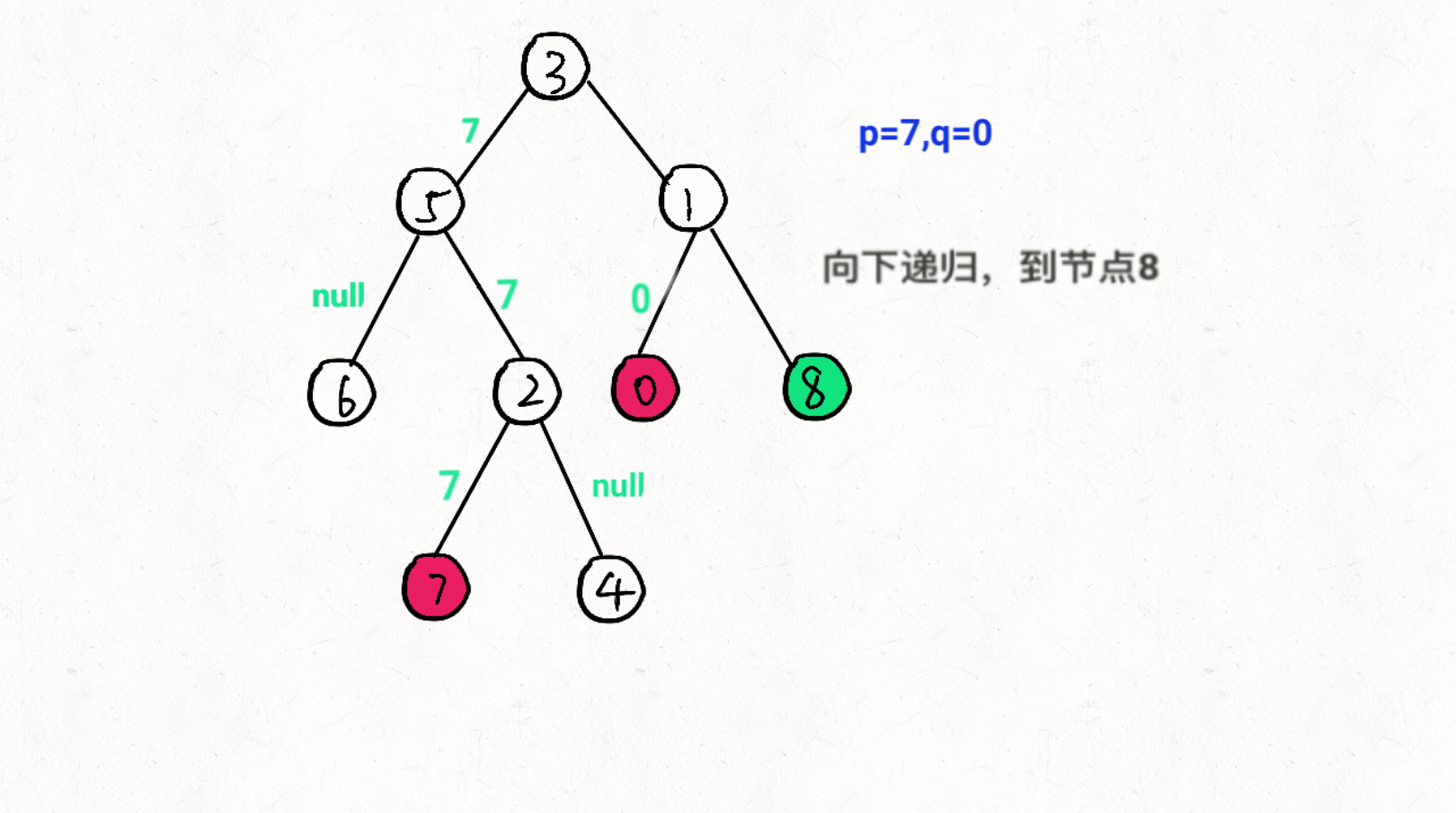
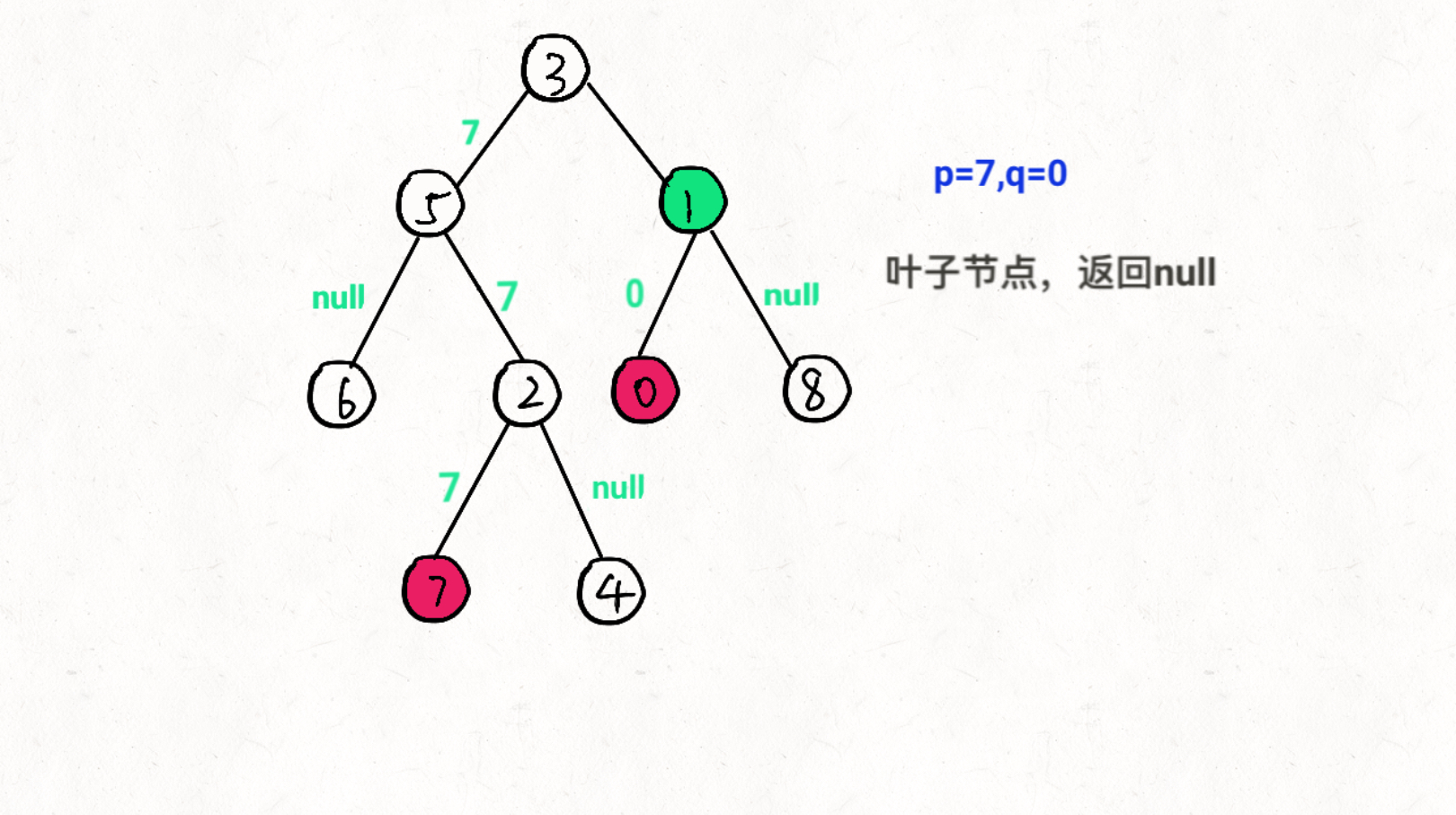
思想:通过递归对二叉树进行后序遍历,当遇到节点 p 或 q 时返回。从底至顶回溯,当节点 p, q 在节点 root 的异侧时,节点root 即为最近公共祖先,则向上返回 root 。
p,q和root有三种情况: 1). p,q在root左右,返回root 2). p,q都在root左,返回
lowestCommonAncestor( root.left, TreeNode p, TreeNode q)3). p,q都在root右,返回lowestCommonAncestor( root.right, TreeNode p, TreeNode q)递归终止条件 if(root == null) return null;//越过叶子节点,返回null if(root == p) return p;//找到p,返回p if(root == q) return q;//找到q,返回q
递归体 递归左子节点,返回值为left
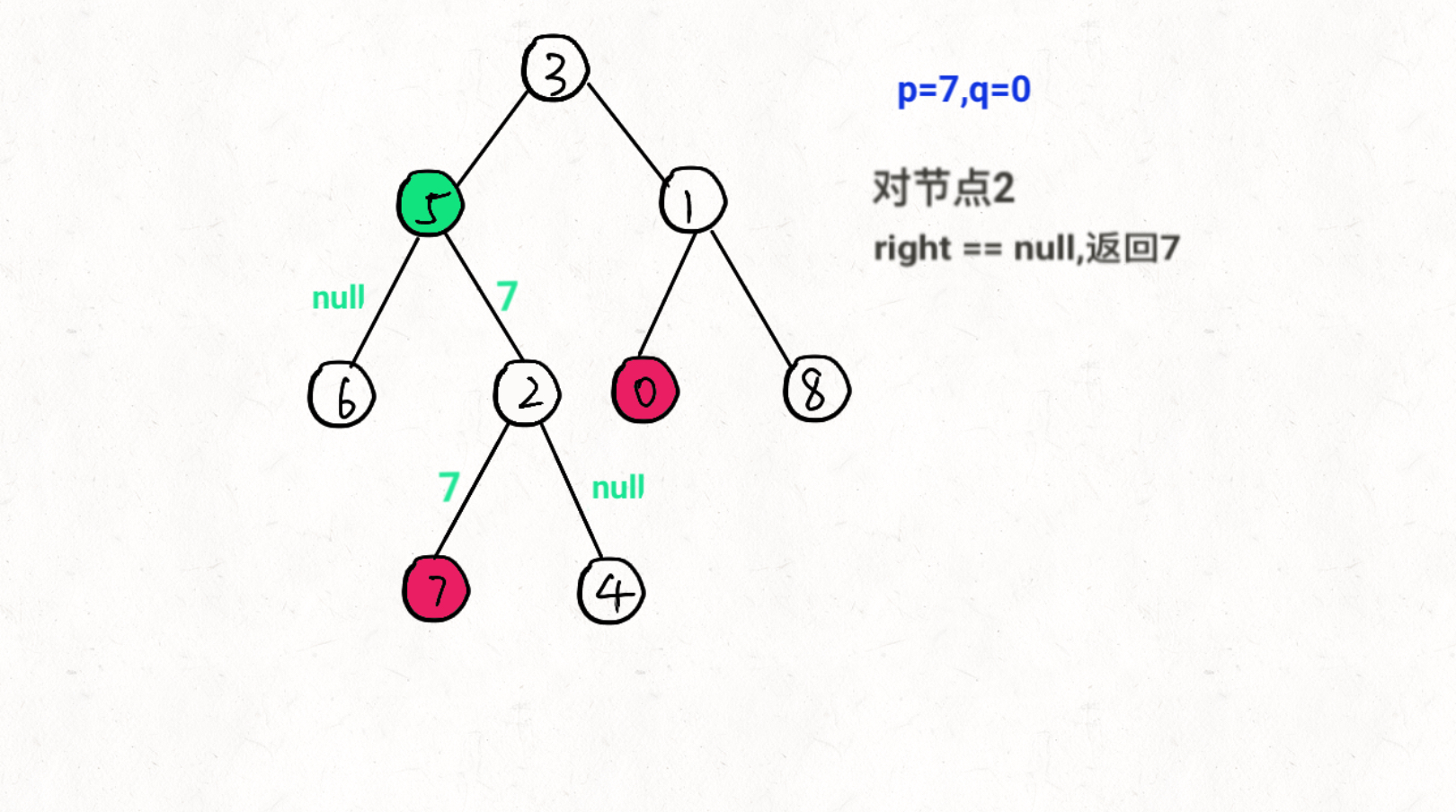
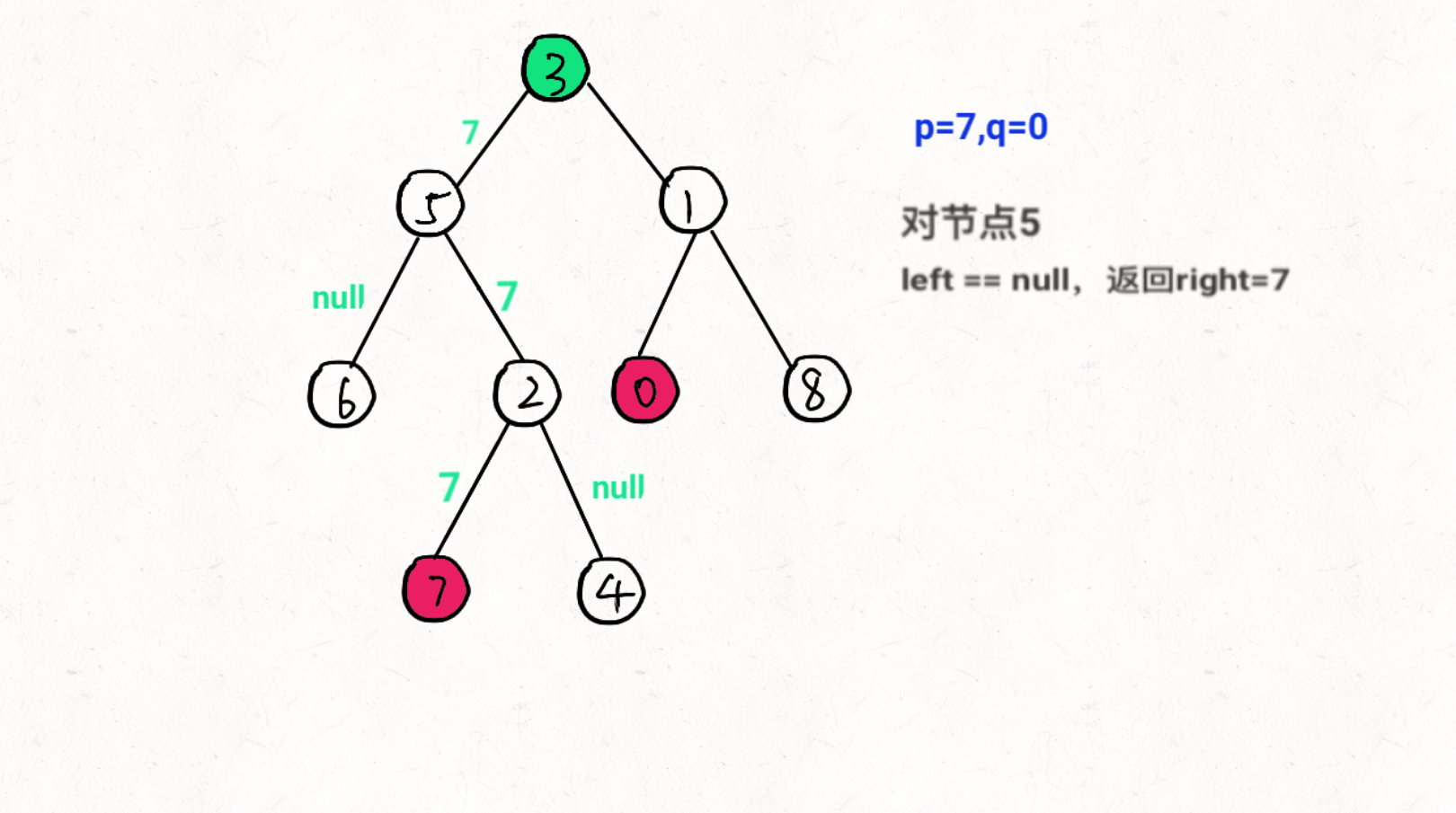
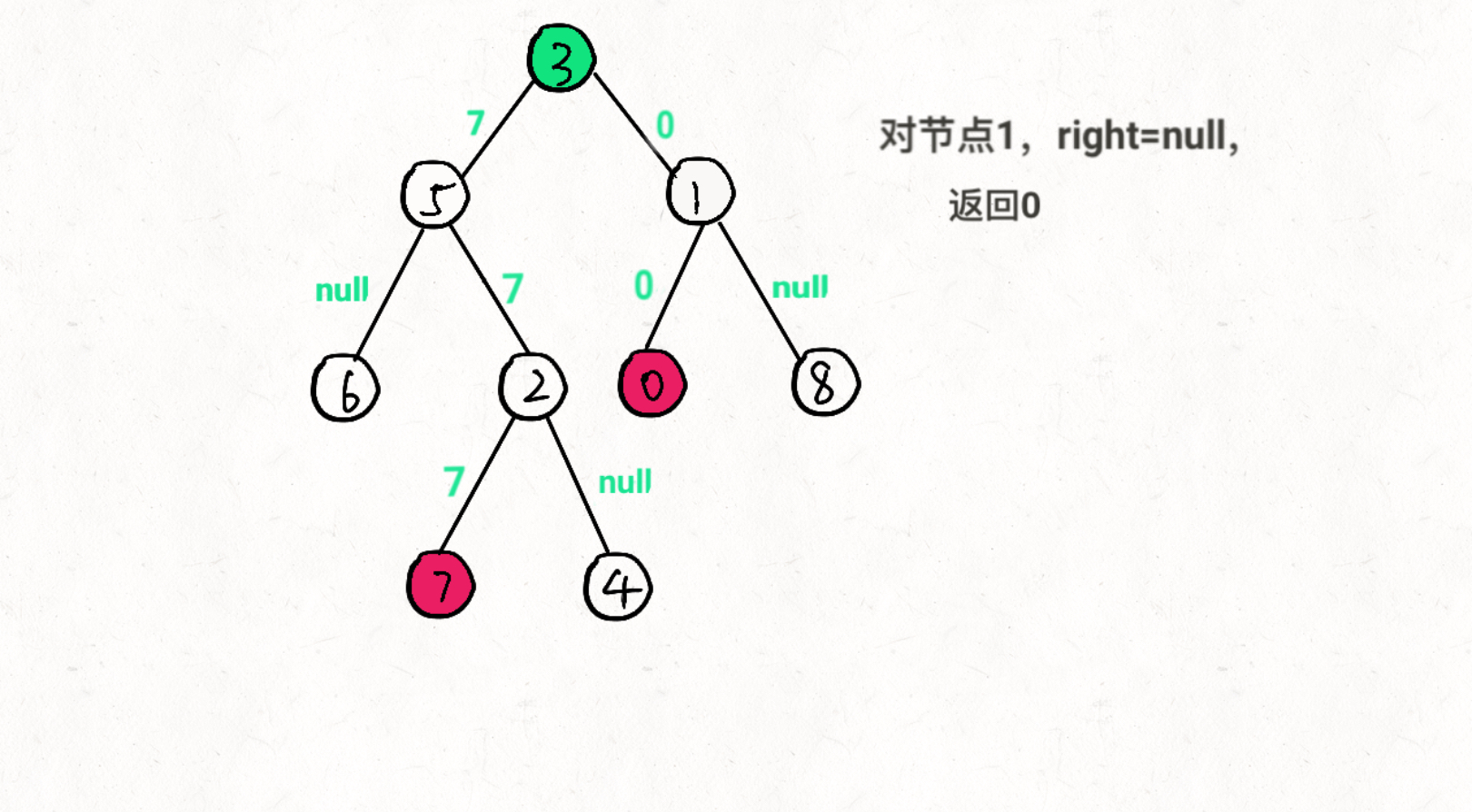
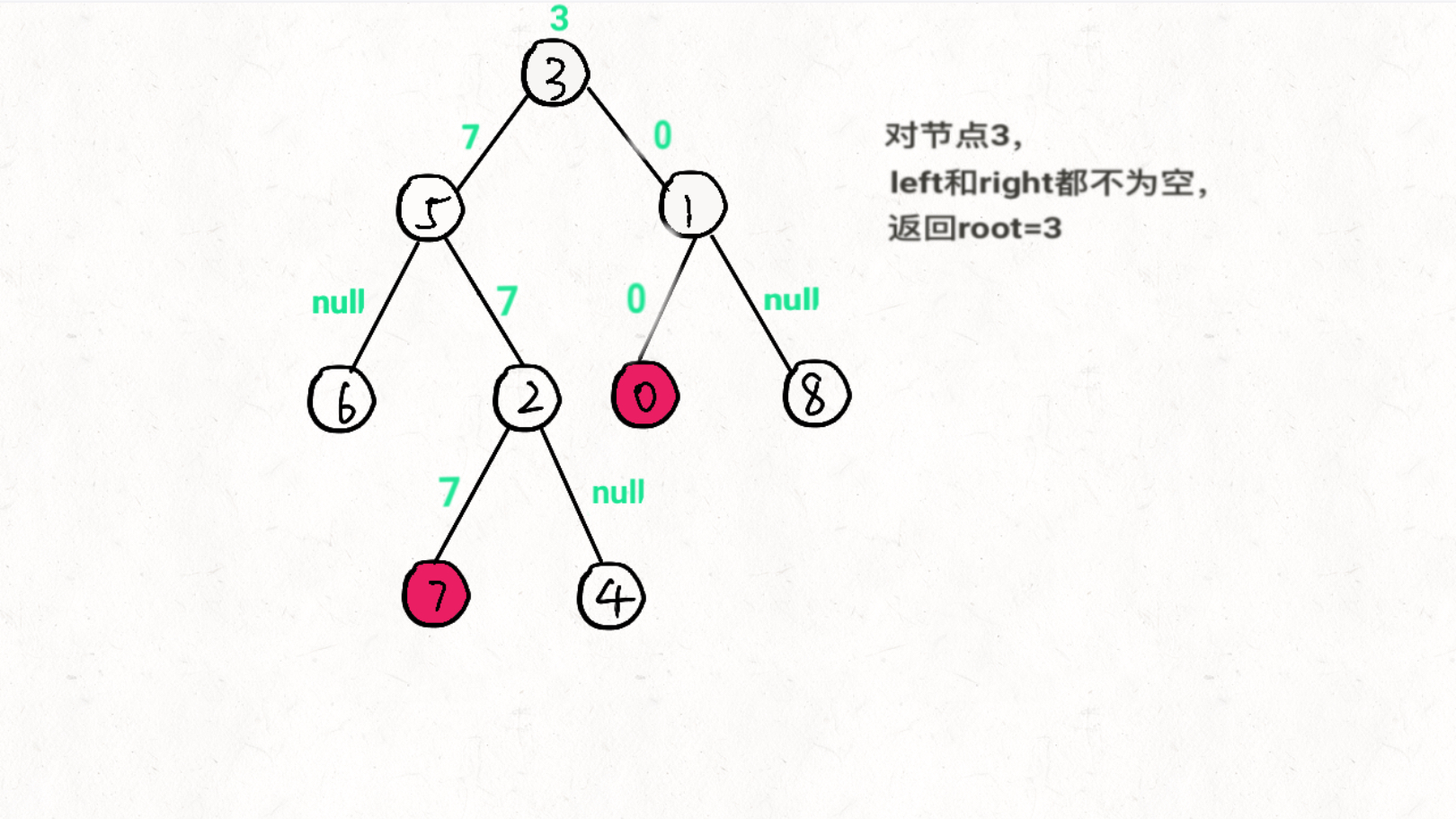
TreeNode left = lowestCommonAncestor( root.left, TreeNode p, TreeNode q);递归右子节点,返回值为rightTreeNode right = lowestCommonAncestor( root.right, TreeNode p, TreeNode q);递归结果 1).left == null && right == null 两边都没找到,返回null 2).left == null 右边找到,返回right 3). right == null 右边找到,返回left 4).left != null && right != null 说明p,q在root两侧,返回root
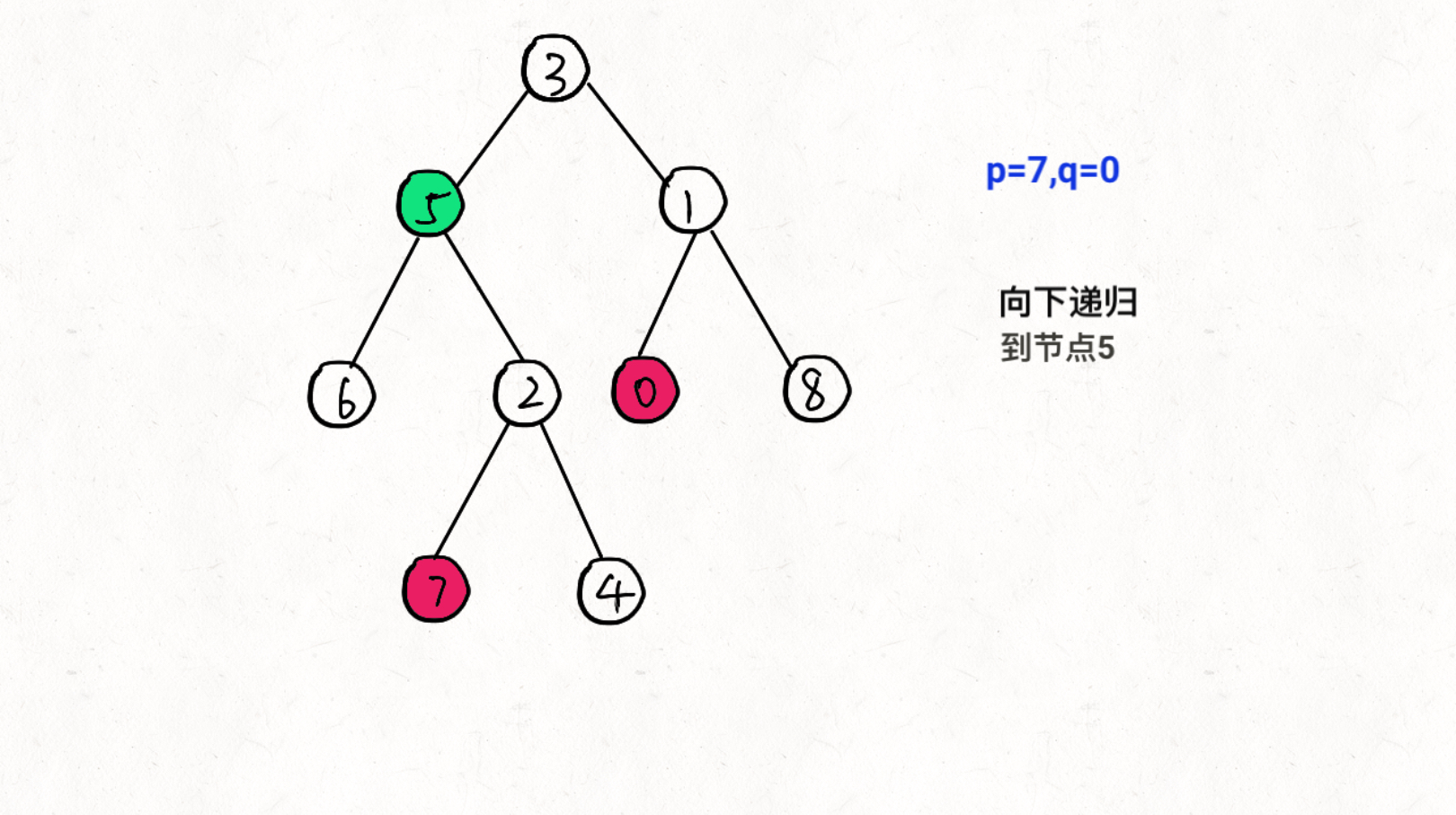
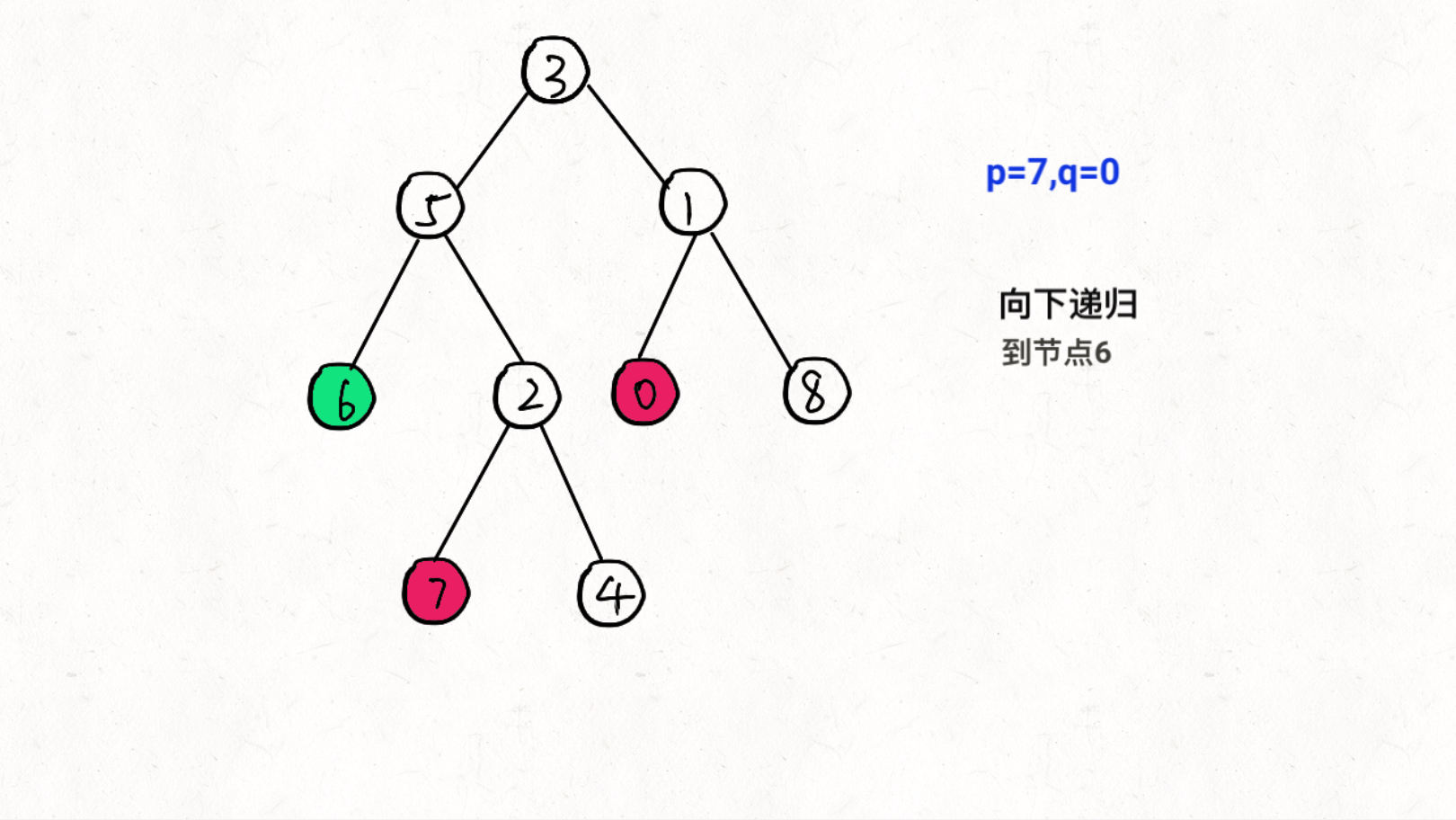
图文过程详解
代码实现
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
//终止条件
if(root == null || root == p || root == q) return root;
//递归体
TreeNode left = lowestCommonAncestor( root.left, p, q);
TreeNode right = lowestCommonAncestor( root.right, p, q);
//递归结果判断-回溯
if(left == null && right == null) return null;
if(left == null) return right;
if(right == null) return left;
return root;
}
}
与上一题相似的机器人运动范围问题
地上有一个m行n列的方格,从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动,它每次可以向左、右、上、下移动一格(不能移动到方格外),也不能进入行坐标和列坐标的数位之和大于k的格子。例如,当k为18时,机器人能够进入方格 [35, 37] ,因为3+5+3+7=18。但它不能进入方格 [35, 38],因为3+5+3+8=19。请问该机器人能够到达多少个格子?
示例 1:
输入:m = 2, n = 3, k = 1 |
示例 2:
输入:m = 3, n = 1, k = 0 |
方法一:递归回溯(DFS)。与上一题类似。
- 递归出口: ① 行列索引越界 或 ② 数位和超出目标值 k 或 ③ 当前元素已访问过
- 递归体:将[i,j]状态设为true,代表已走过,在回溯之后继续走的时候需要避开已走过的方格
- 回溯返回值: 返回 1 + 右方搜索的可达解总数 + 下方搜索的可达解总数
class Solution {
public int movingCount(int m, int n, int k) {
boolean[][] visited = new boolean[m][n];
return dfs(0,0,m,n,k,visited);
}
//计算两个数的位数和
public int sum(int i, int j){
int si = 0, sj = 0;
while(i != 0){
si += i % 10;
i/=10;
}
while(j != 0){
sj += j % 10;
j /= 10;
}
return si + sj;
}
//DFS+回溯
public int dfs(int i, int j, int m, int n, int k, boolean[][] visited){
//递归出口: ① 行列索引越界 或 ② 数位和超出目标值 k 或 ③ 当前元素已访问过
if(i >= m || j >= n || sum(i,j) > k || visited[i][j]) return 0;
//将【i,j】状态设为true,代表已走过,在回溯之后继续走的时候需要避开已走过的方格
visited[i][j] = true;
//回溯返回值: 返回 1 + 右方搜索的可达解总数 + 下方搜索的可达解总数
return 1 + dfs(i + 1, j, m, n, k, visited) + dfs(i, j + 1, m, n, k, visited);
}
}
礼物的最大价值
在一个 m*n 的棋盘的每一格都放有一个礼物,每个礼物都有一定的价值(价值大于 0)。你可以从棋盘的左上角开始拿格子里的礼物,并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值,请计算你最多能拿到多少价值的礼物?
示例 1:
输入: |
方法一:递归回溯。每次只能向右或向下,对每一格的来源只有向左或向上。从右下角开始递归,定义helper方法找到当前位置的礼物最大值。
- 递归出口: ① 行列索引越界 ,返回 0(礼物最小为1) ② 当前元素已访问过 ,返回当前结果
- 递归体:比较左边格子与上边格子的返回结果,取最大值,与当前位置的价值加和。将visited[i,j]状态设为true,代表已走过,在回溯之后继续走的时候需要避开已走过的方格。
- 回溯返回值: 返回 当前位置加和后的结果。
class Solution {
int m ;//行数
int n ;//列数
public int maxValue(int[][] grid) {
m = grid.length;
n = grid[0].length;
if(grid.length == 0 ) return 0;
boolean[][] visited = new boolean[m][n];
return helper(grid, m - 1, n - 1, visited);
}
public int helper(int[][] grid, int i, int j, boolean[][] visited){
//递归出口:边界条件
if(i < 0 || i >= m || j >= n || j < 0) return 0;
//如果已访问过,直接返回
if(visited[i][j] == true) return grid[i][j];
//递归比较当前位置的左边格子与上边格子的返回结果,取最大值
grid[i][j] += Math.max(helper(grid, i - 1, j, visited),helper(grid, i, j - 1, visited));
//并把当前元素状态设为true
visited[i][j] = true;
return grid[i][j];
}
}方法二:动态规划。
结束语
算法小白对递归和回溯的理解只到这里,希望随着刷的题越来越多,理解也越来越清晰透彻,到时再来分享!