深度优先遍历
思想:
对每一个可能的分支路径深入到不能再深入为止,而且每个结点只能访问一次。
二叉树的深度优先遍历
二叉树的深度优先遍历分为前序遍历,中序遍历和后续遍历。
- 前序遍历:先访问根,在访问左子树,最后访问右子树,总结就是“根左右”;
- 中序遍历:先访问左子树,再访问根,最后访问右子树,总结就是“左根右”;
- 后序遍历:先访问左子树,再访问右子树,最后访问根,总结就是“左右根”;
通常采用递归的方式实现遍历,非递归方式需要结合栈(后进先出)的特点实现。
以前序遍历为例:
1. 非递归方式实现(栈)
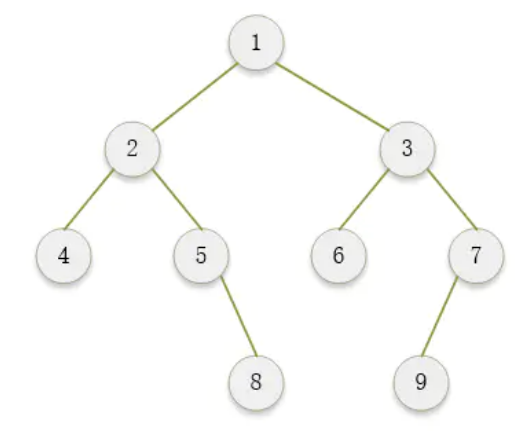
1.1 二叉树结构定义
public static class TreeNode{
int val;
TreeNode left;
TreeNode right;
public TreeNode(int val){
this.val = val;
}
}
|
1.2 创建上图的树
public static TreeNode initTree() {
TreeNode node1 = new TreeNode(1);
TreeNode node2 = new TreeNode(2);
TreeNode node3 = new TreeNode(3);
TreeNode node4 = new TreeNode(4);
TreeNode node5 = new TreeNode(5);
TreeNode node6 = new TreeNode(6);
TreeNode node7 = new TreeNode(7);
TreeNode node8 = new TreeNode(8);
TreeNode node9 = new TreeNode(9);
node1.left = node2;
node1.right = node3;
node2.left = node4;
node2.right = node5;
node3.left = node6;
node3.right = node7;
node5.right = node8;
node7.left = node9;
return node1;
}
|
1.3 非递归方式实现dfs
private static void dfs(TreeNode root) {
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while(!stack.isEmpty()){
TreeNode node = stack.pop();
System.out.print(node.val + " ");
if(node.right != null){
stack.push(node.right);
}
if(node.left != null){
stack.push(node.left);
}
}
}
|
1.4 测试及结果
public static void main(String[] args) {
dfs(initTree());
}
|

2.递归方式实现
public static void dfs(TreeNode root){
if(root == null)
return;
System.out.print(root.val + " ");
dfs(root.left);
dfs(root.right);
}
|
图的深度优先遍历
同样有两种实现方式:递归和非递归。
递归好理解一点,非递归还没摸透,等弄懂了再来填坑~
private void traverse(int i){
vertex[i].visited = true;
System.out.println(vertex[i].getValue());
for(int j=0;j< vertex.length;j++){
if(adjMat[i][j]==1 && vertex[j].visited==false){
traverse(j);
}
}
}
public void dfs(){
for (int i = 0; i < vertex.length; i++) {
vertex[i].visited = false;
}
for(int i=0;i< vertex.length;i++){
if(vertex[i].visited == false){
traverse(i);
}
}
}
|

